81-Graph-Application

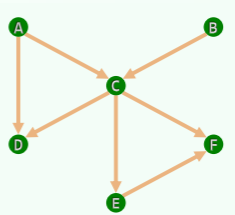
拓扑排序

DAG

有向无环图：Directed Acyclic Graph

应用：
- 类派生和继承关系图中，是否存在循环定义
- 操作系统中相互等待的一组线程，如何调度
- 给定一组相互依赖的课程，设计可行的培养方案
- 给定一组相互依赖的知识点，设计可行的教学进度方案
- 项目工程图中，设计可串行施工的方案
- email 系统中，是否存在自动转发或回复的回路…

拓扑排序的要求

任给有向图 G（不一定是 DAG），尝试将所有顶点排成一个线性序列，使其次序须与原图相容（意即，每一顶点都不会通过边指向前驱顶点）
接口要求：
- 若原图存在回路（即并非 DAG），检查并报告
- 否则，给出一个相容的线性序列

DAG 中的偏序关系

每个 DAG 对应于一个偏序集，而拓扑排序对应于一个全序集，拓扑排序的过程就是构造一个与指定偏序集相容的全序集。
可以拓扑排序的有向图必定无环，反之亦然，DAG 才能做拓扑排序得到线性序列，而且拓扑排序的结果至少一种。
有限的偏序集一定会有极值元素，由此归纳证明可以得到拓扑排序的算法。

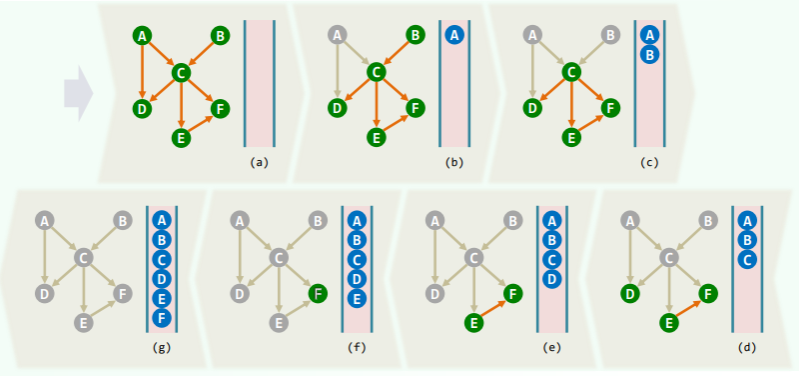
零入度

思路

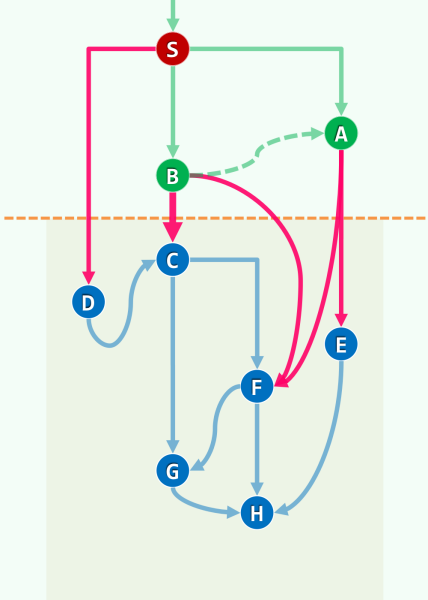
在任何 DAG 中，必有一个零入度的顶点 m，若该 DAG 除去 m 点可以得到一个拓扑排序 S={ $u_{k 1}, u_{k 2}, ..., u_{kn - 1}$ }，则 S’={ $m, u_{k 1}, u_{k 2}, ..., u_{kn - 1}$ }即为该 DAG 的拓扑排序。如此递归下去即可完全排序。

需要注意的是：

DAG 的子图亦为 DAG
只要 m 不唯一，则拓扑排序的结果也不唯一

策略（伪代码）

将所有入度为 0 的顶点存入栈 S，取空队列 Q //O (n)
从栈中输出所有零入度的顶点，最后得到的序列是顺序的零入度顶点：

while ( ! S.empty() ) { //O(n)
	Q.enqueue( v = S.pop() ); //栈顶v转入队列
	for each edge( v, u ) //v的邻接顶点u若入度仅为1
		if ( u.inDegree < 2 ) S.push( u ); //则入栈
	G = G \ { v }; //删除v及其关联边（邻接顶点入度减1）
} //总体O(n + e)
return |G| ? "NOT_A_DAG" ： Q; //残留的G空，当且仅当原图可拓扑排序

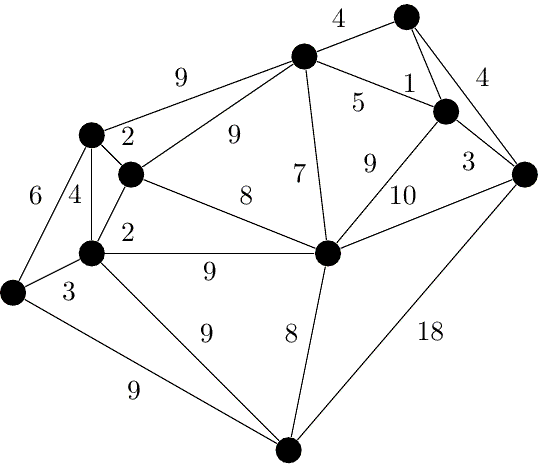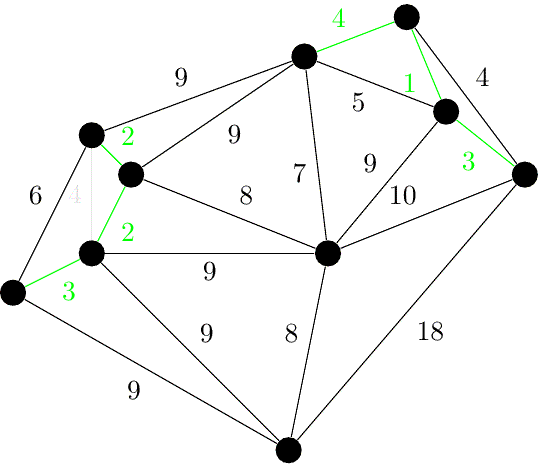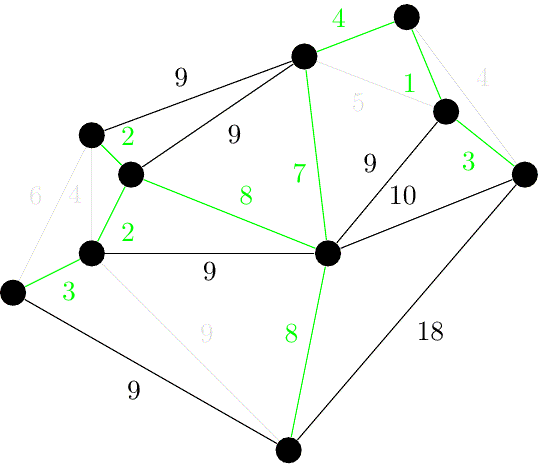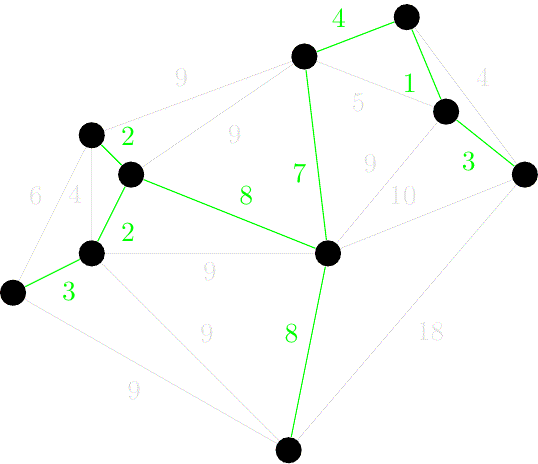
实例

零出度

思路

相对应地，可以从 DAG 的零出度顶点逆向出发，递归地输出所有 DAG 及其子图的零出度顶点。

策略（描述）

基于 DFS，借助栈 S，对图 G 做 DFS，得到组成 DFS 森林的一系列 DFS 树
其间每当有顶点被标记为 VISITED，则将其压入 S，一旦发现有后向边，则报告“NOT_A_DAG”并退出 (出现了环，不再是 DAG)
DFS 结束后，顺序弹出 S 中的各个顶点

各节点按 fTime 逆序排列，即是（零出度）拓扑排序 //因为 ftime 代表对一个顶点的访问结束，其在当前子图中不再有出度。

整体算法的复杂度与 DFS 相当，也是 O (n+e)

实例

代码

//基于DFS的拓扑排序算法（全图）
template <typename Tv, typename Te>
Stack<Tv>* Graph<Tv, Te>::tSort( Rank s ) { // assert: 0 <= s < n
	reset(); Rank clock = 0; //全图复位
	Stack<Tv>* S = new Stack<Tv>; //用栈记录排序顶点
	for ( Rank v = s; v < s + n; v++ ) //从s起顺次检查所有顶点
	    if ( UNDISCOVERED == status( v % n ) ) //一旦遇到尚未发现者
	        if ( !TSort( v, clock, S ) ) { //即从它出发启动一次TSort
		        while ( !S->empty() ) //任一连通域（亦即整图）非DAG
		            S->pop();
	            break; //则不必继续计算，故直接返回
	        }
	return S; //若输入为DAG，则S内各顶点自顶向底排序；否则（不存在拓扑排序），S空
} //如此可完整覆盖全图，且总体复杂度依然保持为O(n+e)


//基于DFS的拓扑排序算法（单连通图）
template <typename Tv, typename Te>
bool Graph<Tv, Te>::TSort( Rank v, Rank& clock, Stack<Tv>* S ) { // v < n
	dTime( v ) = ++clock; status( v ) = DISCOVERED; //发现顶点v
	for ( Rank u = firstNbr( v ); - 1 != u; u = nextNbr( v, u ) ) //枚举v的所有邻居u
	    switch ( status( u ) ) { //并视u的状态分别处理
	        case UNDISCOVERED :
		        parent( u ) = v; type( v, u ) = TREE;
		        if ( !TSort( u, clock, S ) ) //从顶点u处出发深入搜索
		            return false; //若u及其后代不能拓扑排序（则全图亦必如此），故返回并报告
	            break;
	        case DISCOVERED :
	            type( v, u ) = BACKWARD; //一旦发现后向边（非DAG），则
	            return false; //不必深入，故返回并报告
	        default : // VISITED (digraphs only)
		        type( v, u ) = ( dTime( v ) < dTime( u ) ) ? FORWARD : CROSS;
	            break;
	    }
	status( v ) = VISITED; S->push( vertex( v ) ); //顶点被标记为VISITED时，随即入栈
	return true; // v及其后代可以拓扑排序
}

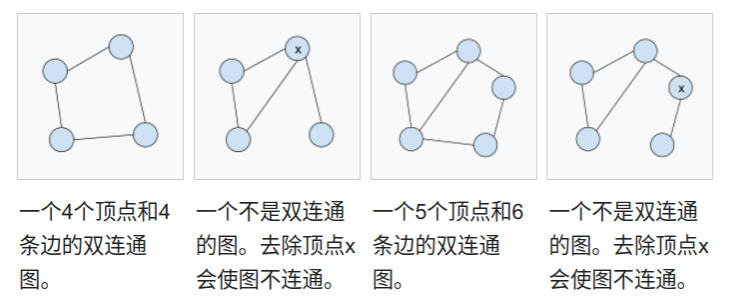
双连通分量

判定

定义

无向图的关节点 (articulation point, cut-vertex)：其删除之后，原图的连通分量增多
无关节点的图，称作双（重）连通图 (bi-connectivity)：任何一个顶点被去除，图仍是连通的
极大的双连通子图，称作双连通分量 (Bi-Connected Components, BCC)

暴力法

确定一个无向图的各 BCC，如果使用暴力法，则逐个拆除关节点：

对每一顶点 v，通过遍历检查 G\{v} 是否仍连通；
这一方法需要 O (n*(n+e)的时间，并且找出关节点后仍需遍历重新确定 BCC

改进：利用 DFS

构造 DFS 树，根据 DFS 留下的标记，甄别是否是关节点：

叶节点绝不是关节点——删除后对全树（图）的连通性没有影响；
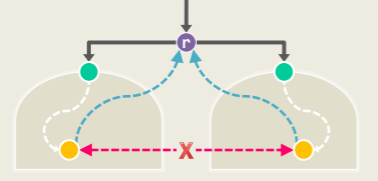
考查非叶节点，若其是关节点，则必须有如下条件：
- 对根 r，其必须有至少 2 棵子树：
- 对内部节点 v，其有某个孩子 u，u 的子树不能经由 BACKWARD 边连接到 v 的任何真祖先 a（即取掉 v 也能通过 BACKWARD 连回到a）：
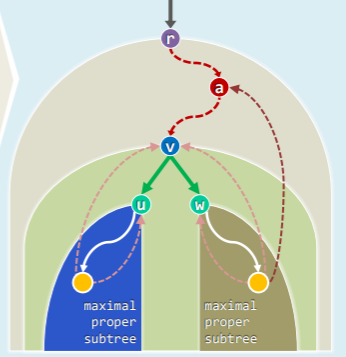
  - 此时{v}= $BCC (u) \cap BCC (p a re n t (v))$
  - 记最高可达祖先 hca(v) ，表示 subtree (v)中节点经 BACKWARD 可达的最高祖先：
    - 由括号引理，可以知道 dTime 越小的祖先，辈分越高，其中 dTime=0 的祖先为根节点
    - 在 DFS 过程中，一旦发现<v, u>是 BACKWARD，则取 hca (v)=min (hac (v), dTime (u))
    - 当 DFS (u)完成并返回到 v 时，若有 hca (u)<dTime (v)，则取 hca (v)=min (hca (v), hca (u))
    - 否则即可断定 v 是关节点，且{v}+subtree (u)即为一个 BCC

代码

//基于DFS的BCC分解算法(全图)
template <typename Tv, typename Te>
void Graph<Tv, Te>::bcc( Rank s ) { 
	reset(); Rank clock = 0; Rank v = s; 
	Stack<Rank> S; //栈S用以记录已访问的顶点
	do
	    if ( UNDISCOVERED == status( v ) ) { //一旦发现未发现的顶点（新连通分量）
	        BCC( v, clock, S ); //即从该顶点出发启动一次BCC
	        S.pop(); //遍历返回后，弹出栈中最后一个顶点――当前连通域的起点
	    }
	while ( s != ( v = ( ++v % n ) ) );
}

#define hca(x) (fTime(x)) //利用此处闲置的fTime[]充当hca[]
template <typename Tv, typename Te> //顶点类型、边类型
void Graph<Tv, Te>::BCC( Rank v, Rank& clock, Stack<Rank>& S ) { // assert: 0 <= v < n
	hca( v ) = dTime( v ) = ++clock; 
	status( v ) = DISCOVERED; 
	S.push( v ); // v被发现并入栈
	
	for ( int u = firstNbr( v ); - 1 != u; u = nextNbr( v, u ) ) //枚举v的所有邻居u
	    switch ( status( u ) ) { //并视u的状态分别处理
	        case UNDISCOVERED:
	            parent( u ) = v; type( v, u ) = TREE;
	            BCC( u, clock, S ); //从顶点u处深入
	            if ( hca( u ) < dTime( v ) ) //遍历返回后，若发现u（通过后向边）可指向v的真祖先
		            hca( v ) = min( hca( v ), hca( u ) ); //则v亦必如此
	            else //否则，以v为关节点（u以下即是一个BCC，且其中顶点此时正集中于栈S的顶部）
		            while ( u != S.pop() ); //弹出当前BCC中（除v外）的所有节点，可视需要做进一步处理
	            break;
	        case DISCOVERED:
	            type( v, u ) = BACKWARD; //标记(v, u)，并按照“越小越高”的准则
			    if ( u != parent( v ) ) 
				    hca( v ) = min( hca( v ), dTime( u ) ); //更新hca[v],越小越高
	            break;
	        default: //VISITED (digraphs only)
	            type( v, u ) = ( dTime( v ) < dTime( u ) ) ? FORWARD : CROSS;
		        break;
	    }
	status( v ) = VISITED; //对v的访问结束
}
#undef hca

复杂度

运行时间与常规的 DFS 相同，也是 O (n + e) ，栈操作的复杂度也不过如此
除原图本身，还需一个容量为 O (e)的栈存放已访问的边
为支持递归，另需一个容量为 O (n)的运行栈

如何推广至有向图的强连通分量（Strongly-connected component）？

Kosaraju’s algorithm
Tarjan’s algorithm

实例

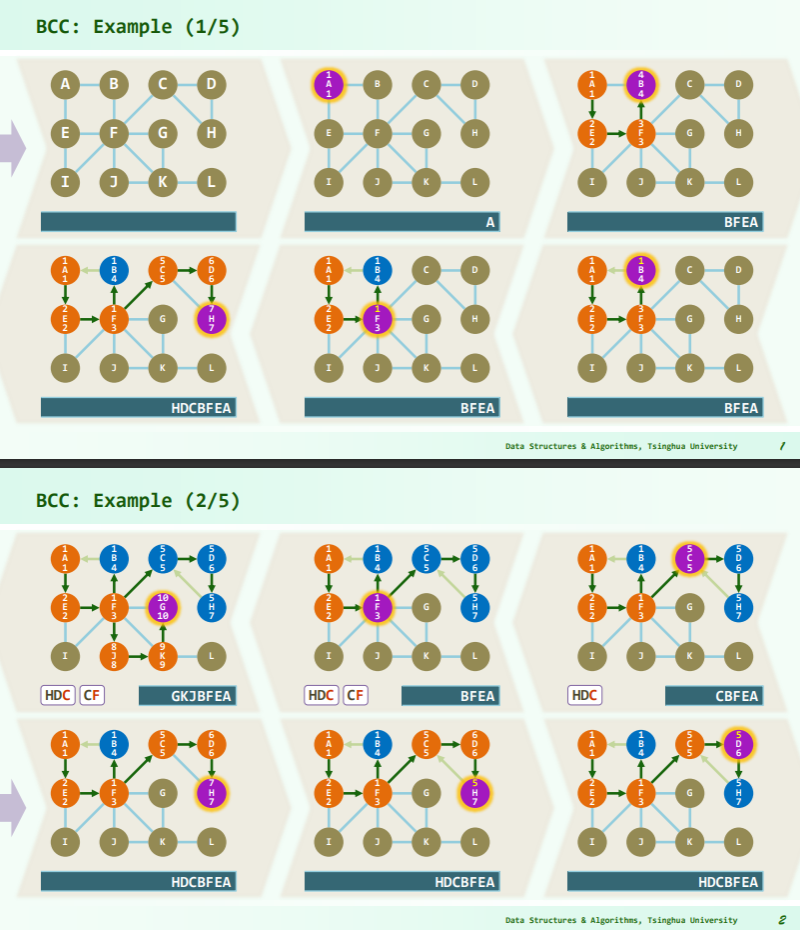
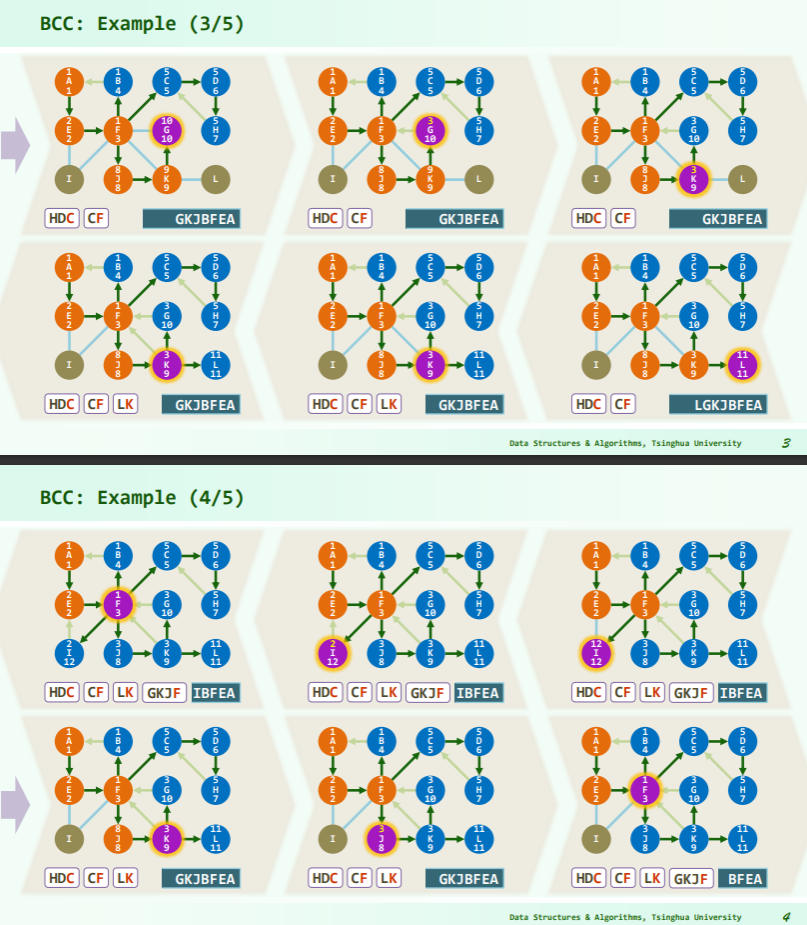
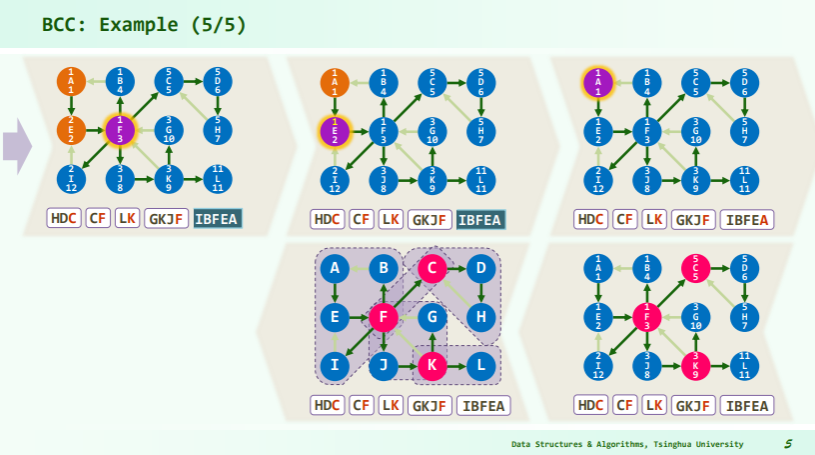
[! note] 如何判断根节点是否为关节点？这个实例在最后一步判断出发节点 A 是否为关节点时，先将 A 当作关节点处理，再又祛除。但是在代码中不能排除 dfs 根不是关节点的情况，因为算法是 dtime>＝hca，就会被认成关节点，而不会有 hca 小于根节点的 dtime。

一种比较好的解决思路是：统计根节点的出度——根节点出度为 1 时，必然不会是关节点，而出度为 2 时又必然是关机点。

优先级搜索

各种遍历算法的区别，仅在于选取顶点进行访问的次序：

广度/深度：优先访问与更早/更晚被发现的顶点相邻接者；
不同的遍历算法，取决于顶点的选取策略，不同的顶点选取策略，取决于存放和提供顶点的数据结构
PFS 的思想就是为每个顶点 v 维护一个优先级数 priority (v)，每次选取访问的节点依据于 priority:
- 每个顶点都有初始优先级数，并可能随算法的推进而调整
- 通常的习惯是，优先级数越大/小，优先级越低/高, 特别地，priority (v) == INT_MAX，意味着 v 的优先级最低

由此 PFS 可以作为一个算法框架，容纳很多对图的不同遍历需求。

算法框架

template <typename Tv, typename Te> 
template <typename PU> //优先级搜索（全图）
void Graph<Tv, Te>::pfs( Rank s, PU prioUpdater ) { // s < n
	reset(); //全图复位
	for ( Rank v = s; v < s + n; v++ ) //从s起顺次检查所有顶点
	    if ( UNDISCOVERED == status( v % n ) ) //一旦遇到尚未发现者
	        PFS( v % n, prioUpdater ); //即从它出发启动一次PFS
} //如此可完整覆盖全图，且总体复杂度依然保持为O(n+e)

template <typename Tv, typename Te>
template <typename PU> //顶点类型、边类型、优先级更新器
void Graph<Tv, Te>::PFS( Rank v, PU prioUpdater ) { //优先级搜索（单个连通域）
	priority( v ) = 0;
	status( v ) = VISITED; //初始化，起点v加至PFS树中
	
	while ( 1 ) { //将下一顶点和边加至PFS树中
	    for ( Rank u = firstNbr( v ); - 1 != u; u = nextNbr( v, u ) ) //对v的每一个邻居u
	        prioUpdater( this, v, u ); //更新其优先级及其父亲
	    int shortest = INT_MAX;
	    for ( Rank u = 0; u < n; u++ ) //从尚未加入遍历树的顶点中，选出下一个优先级
	        if ( ( UNDISCOVERED == status( u ) ) && ( shortest > priority( u ) ) ) //最高的
	            { shortest = priority( u ), v = u; } //顶点v
	    if ( shortest == INT_MAX ) break; //直至所有顶点均已加入
	    status( v ) = VISITED; type( parent( v ), v ) = TREE; //将v加入遍历树
	}//while
} //通过定义具体的优先级更新策略prioUpdater，即可实现不同的算法功能

复杂度

执行时间主要消耗于内、外两重循环；其中两个内循环前、后并列
- 前一内循环的累计执行时间：若采用邻接矩阵，为 O (n^2)；若采用邻接表，为 O (n+e)
- 后一循环中，优先级更新的次数呈算术级数变化{ n, n - 1, …, 2, 1 }，累计为 O (n^2) ,两项合计，为 O (n^2)
后面可以改进：若采用优先级队列，以上两项将分别是 O (elogn)和 O (nlogn) ，两项合计，为 O ((e+n) logn)
- 这是很大的改进——尽管对于稠密图而言，反而是倒退 //已有接近于 O (e + nlogn)的算法
- 基于这个统一框架，可以解决一系列应用问题。

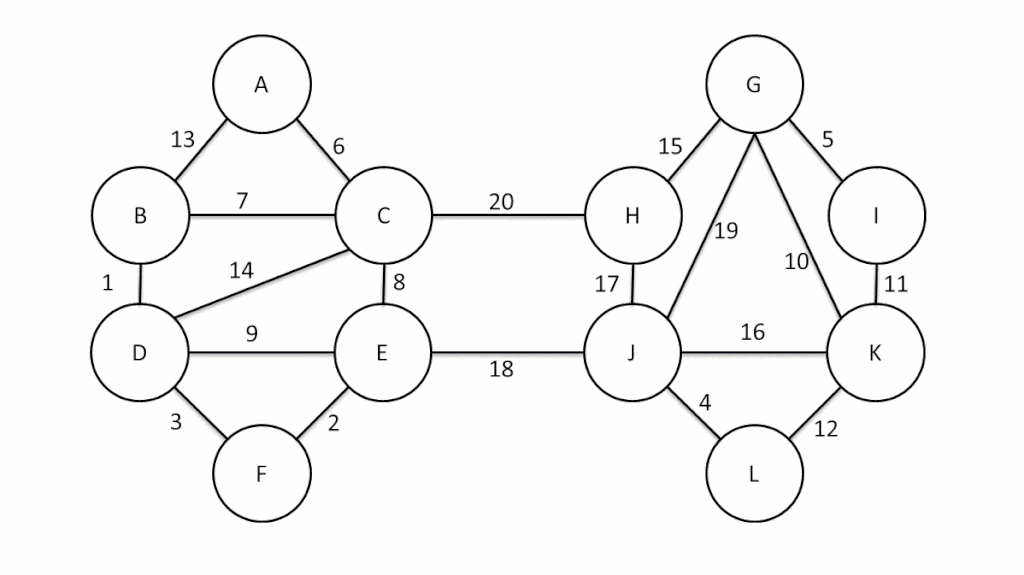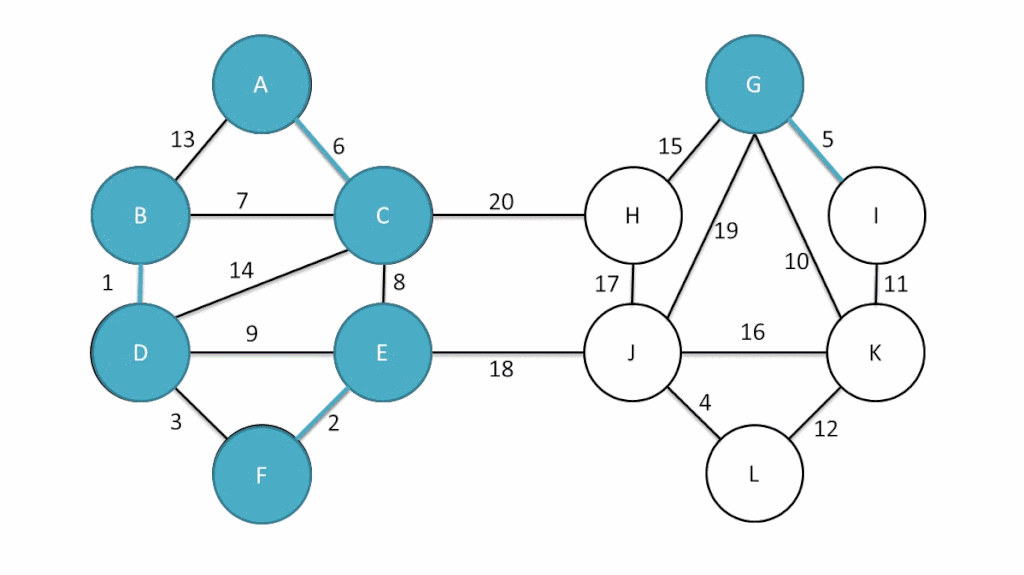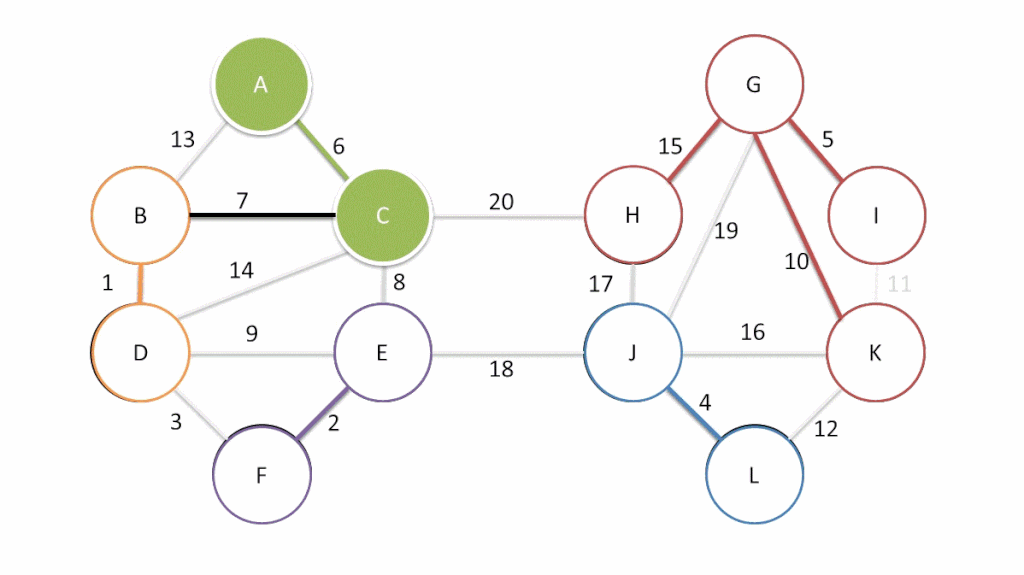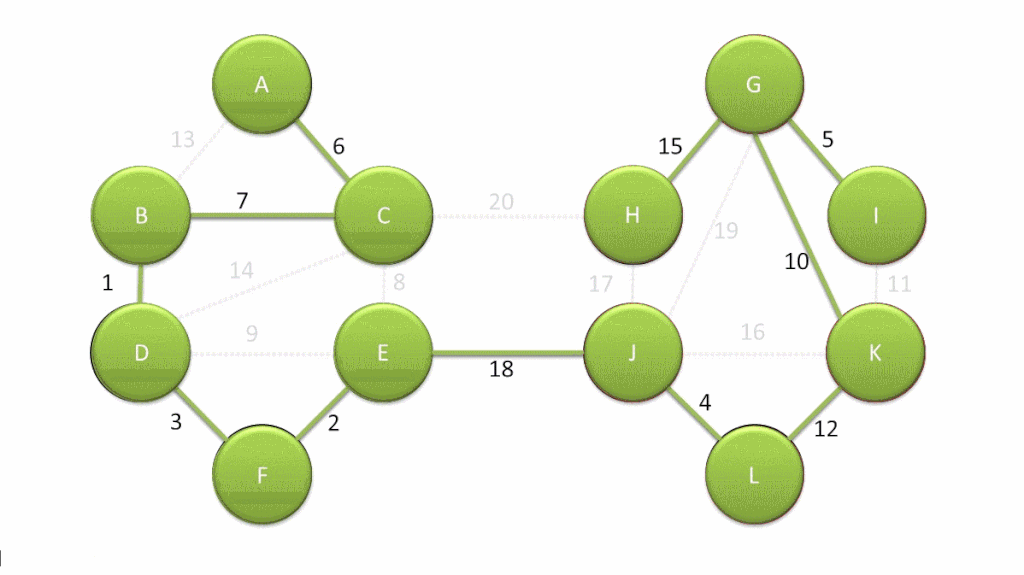
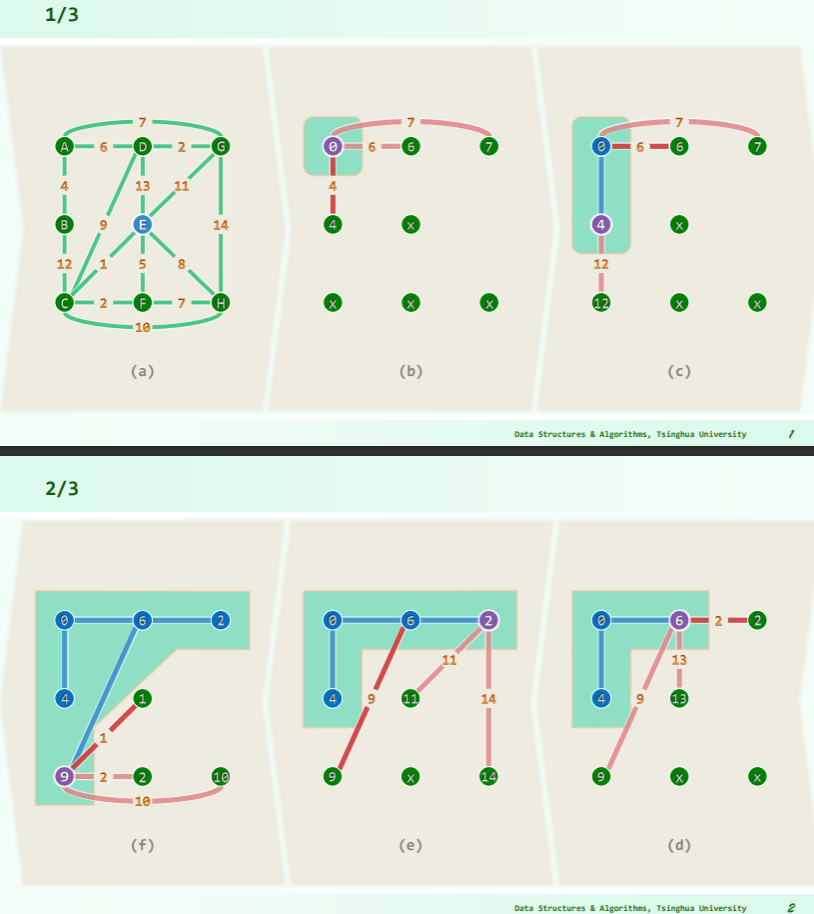
Dijkstra 算法求最短路径

问题描述

在给定有向连通图 G 及其中顶点 u 和 v，如何找到从 u 到 v 的最短路径？

这个问题应用广泛：

旅游者：最经济的出行路线
路由器：最快地将数据包传送到目标位置
路径规划：多边形区域内的自主机器人

按照图的类型，可以划分为无权图、带权有向图（目前讨论的权值为非负，实际上负权值可以给每个权都加一个正数，使其非负再做讨论，最后减去这个整数就好）：

Dijkstra 于 1959 年给出算法 SSSP (Single-Source Shortest Path)：给定顶点 s，计算 s 到其余各个顶点的最短路径及长度；
Floyd-Warshall 于 1962 年给出 APSP (All-Pairs Shortest Path)：找出每对顶点 v 和 u 之间的最短路径及长度。

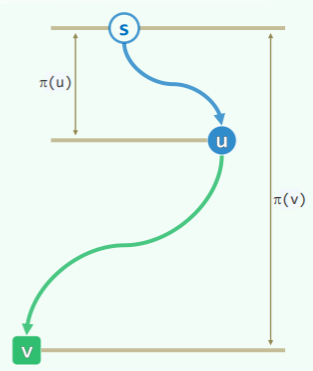
最短路径树

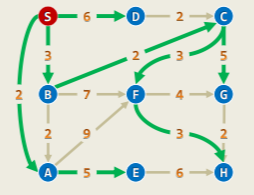
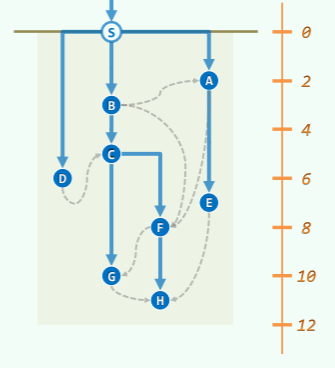
对于两点间最短路径问题，可以确定：任一最短路径的前缀，也必然是最短路径。如下图，将<s, v>的最短路径记作 $π (v)$ ，则有：

$u \in π (v) ⟺ π (u) \subseteq π (v)$

另外，在以 Dijkstra 方法构建最短路径树之前，需要明确：

各边权重均为正，否则有可能出现总权重非正的环路，以致最短路径无从定义
有负权重的边时，即便所有环路总权重皆为正，Dijkstra 算法依然可能失效
任意两点之间，最短路径唯一，在不影响计算结果的前提下，总可通过适当扰动予以保证（习题 6-17）

最短路径树 SPT：是所有最短路径的并集，并且继承了树的性质——极小连通图，最大无环图：

$T = T_{n - 1} = 0 \leq i < n ⋃ π (u_{i})$ 构成的一棵树

算法

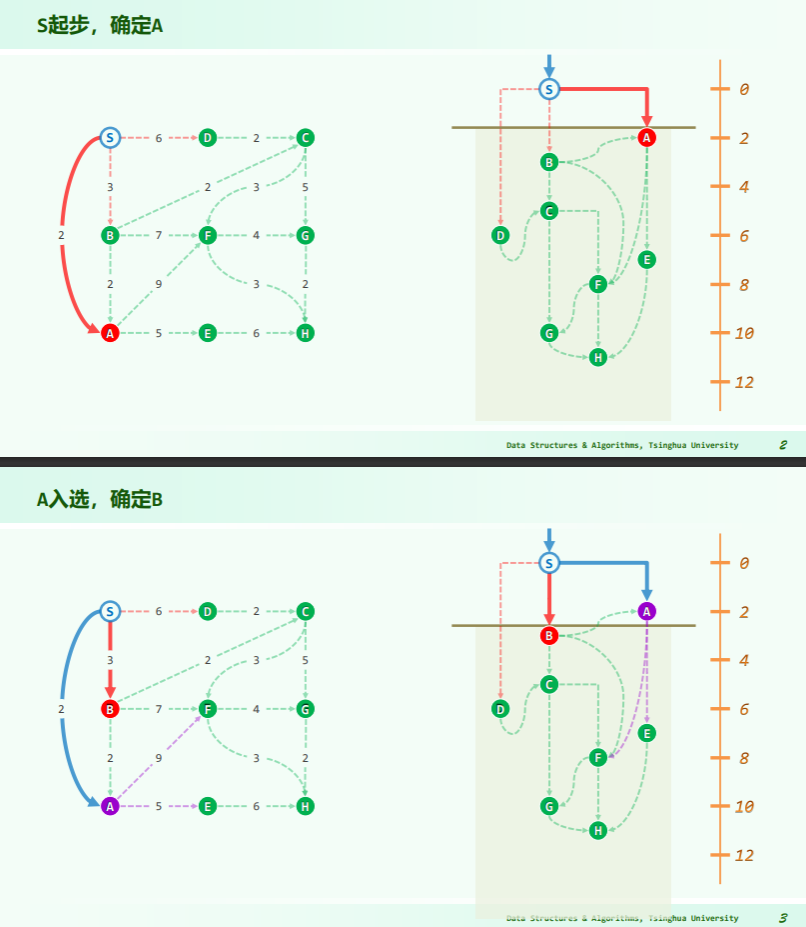
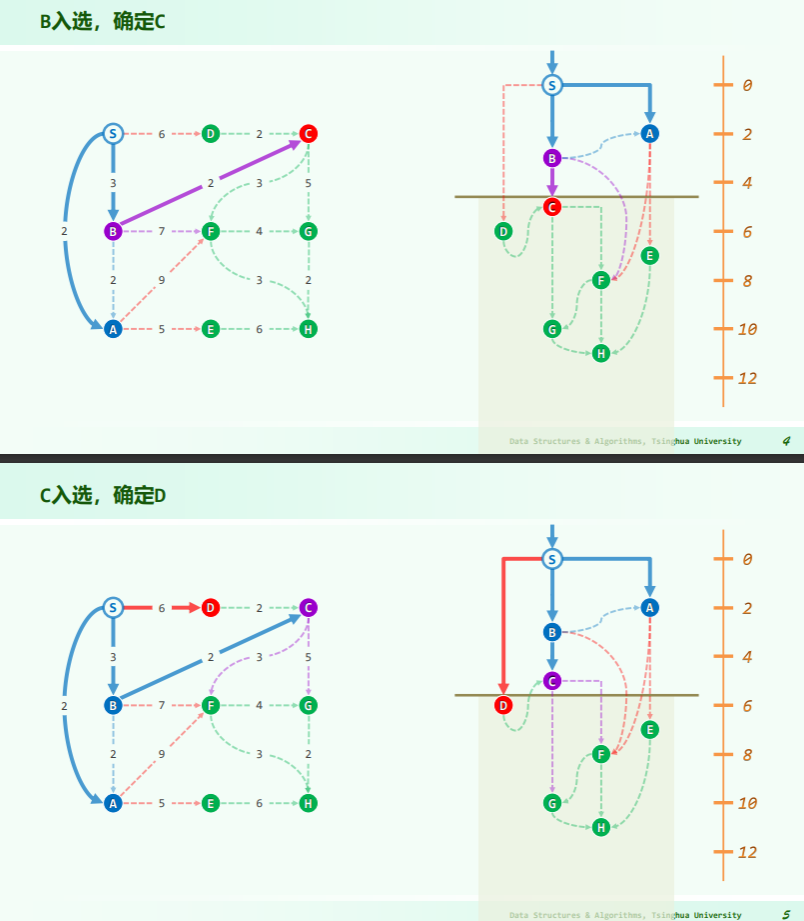
思路：减治，每一次遍历都减小一次搜索范围：

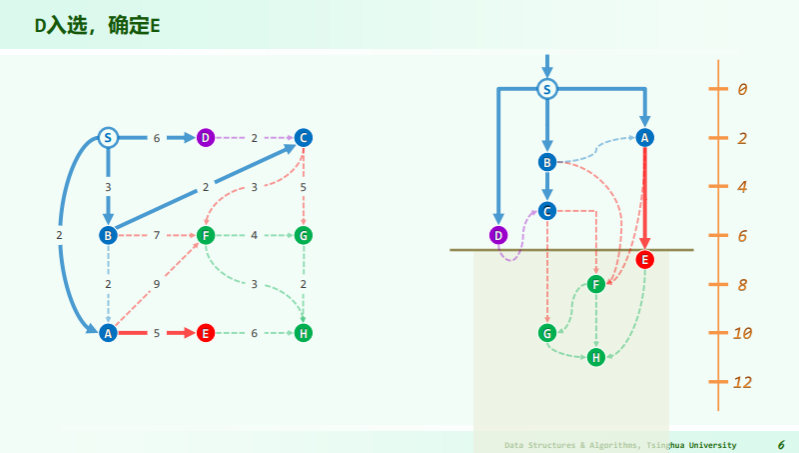
实例

实现

在图 G 及其子图中，每一轮都为可在一条路径到达的节点标记优先级 priority，其值决定于已确定范围到目标点的距离；
套用 PFS 框架，每一轮 SPT 的增长： $T_{k} \Rightarrow T_{k + 1}$ ，
1. 只需要选出优先级最高的跨边 CROSS及其对应顶点 $u_{k}$ ，
2. 将其接入 $T_{k}$ 即可，随后再更新 $V V_{k + 1}$ 中所有顶点的优先级；
需要注意，优先级随后可能改变（降低）的顶点，必定与 $u_{k}$ 邻接；
因此只需枚举 $u_{k}$ 的每一邻接顶点 $v$ ，并取 $p r i or i t y (v) = min (p r i or i t y (v), p r i or i t y (u_{k}) + ∣∣ u_{k}, v ∣∣)$

因此对应于 Dijkstra 的优先级更新器如下：

//针对Dijkstra算法的顶点优先级更新器
template <typename Tv, typename Te> struct DijkPU { 
	virtual void operator()( Graph<Tv, Te>* g, Rank v, Rank u ) {
	    if ( UNDISCOVERED == g->status( u ) ) //对于v每一尚未被发现的邻接顶点u，按Dijkstra策略
	        if ( g->priority( u ) > g->priority( v ) + g->weight( v, u ) ) { //做松弛
		        g->priority( u ) = g->priority( v ) + g->weight( v, u ); //更新优先级（数）
	            g->parent( u ) = v; //并同时更新父节点
	        }
	}
};

整体 Dijkstra 算法如下：

//最短路径Dijkstra算法：适用于一般的有向图
template <typename Tv, typename Te>
void Graph<Tv, Te>::dijkstra( Rank s ) { // s < n
   reset(); priority( s ) = 0;
   for ( Rank i = 0; i < n; i++ ) { //共需引入n个顶点和n-1条边
      status( s ) = VISITED;
      if ( -1 != parent( s ) ) type( parent( s ), s ) = TREE; //引入当前的s
      for ( Rank j = firstNbr( s ); - 1 != j; j = nextNbr( s, j ) ) //枚举s的所有邻居j
         if ( ( status( j ) == UNDISCOVERED ) && ( priority( j ) > priority( s ) + weight( s, j ) ) ) //对邻接顶点j做松弛
            { priority( j ) = priority( s ) + weight( s, j ); parent( j ) = s; } //与Prim算法唯一的不同之处
      int shortest = INT_MAX;
      for ( Rank j = 0; j < n; j++ ) //选出下一最近顶点
         if ( ( status( j ) == UNDISCOVERED ) && ( shortest > priority( j ) ) )
            { shortest = priority( j ); s = j; }
   }
} //对于无向连通图，假设每一条边表示为方向互逆、权重相等的一对边

Prim 算法求 MST

MST 是什么

支撑：对连通网络 N=(V; E)的子图 T=(V; F)，所谓支撑指的是覆盖 N 中所有可达顶点。树即可做到——连通且无环，并且树边数|F| = |V|-1；
最小：总权重 $w (T) = e \in F \sum w (e)$ 达到最小
- MST 的优势应用：众多优化问题的基本模型，为许多 NP 问题提供足够好的近似解

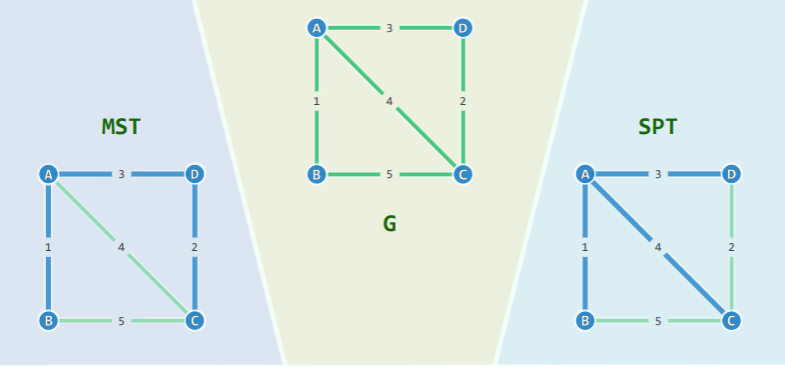
MST != SPT

MST：针对子图总距离最短
SPT：针对所求点距离最短

在考虑 MST 之前，需要确定：

权值必须是正数？
- 允许为零，有何影响？
- 允许为负数呢？
支撑树虽然可以有很多种，但所含的边数必然是相同的：|V|-1
存在权重相同的边的图中，构造的 MST 可能有多种，为了消除歧义，可以考虑对节点的信息也加入权重考量中：

蛮力算法

枚举出 N 的所有支撑树，再逐个计算代价
但是包含 n 个顶点的图，可能有多少棵支撑树？
- n=1 1
- n=2 1
- n=3 3
- n=4 16
- n=5 125…
[Cayley]( http://en.wikipedia.org/wiki/Cayley ‘s_formula) 公式：完全图 $K_{n}$ 有 $n^{n - 2}$ 棵支撑树

改进思路：极短跨边

排除环路中最长边
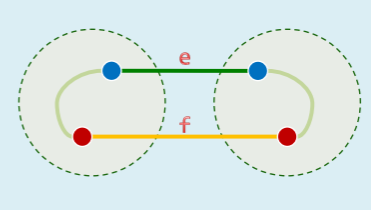
观察，任何环路 C 上的最长边 f，都不会被 MST 采用，否则都会有一个更短的边 e 取代之：
- 移除 f 后，MST 分裂为两棵树，将其视作一个割¹，
- 则 C 上必有该割的另一跨边 e，既然|e|<|f|，那么只要用 e 替换 f，就会得到一棵总权重更小的支撑树；（Kruskal 算法的依据）

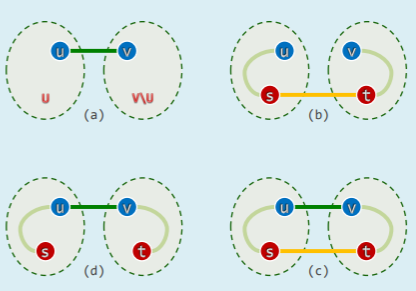
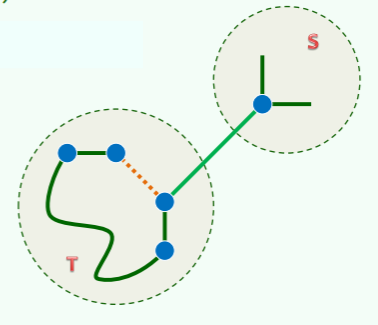
容纳割的最短边
设 (U; V\U)是 N 的一个割，若 uv 是该割的一条极短跨边，则必存在一棵包含 uv 的 MST（Prim 算法的依据）
反证：假设 uv 未被任何 MST 采用，任取一棵 MST，将 uv 加入其中，于是
- 将出现唯一的回路，
- 且该回路必经过 uv 以及至少另一跨边 st
- 接下来，摘除 st 后又恢复为一棵支撑树，且总权重不致增加
- 反之，任一 MST 都必然通过极短跨边联接每一割

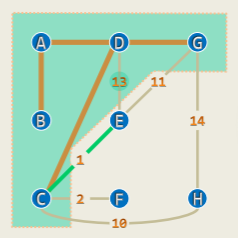
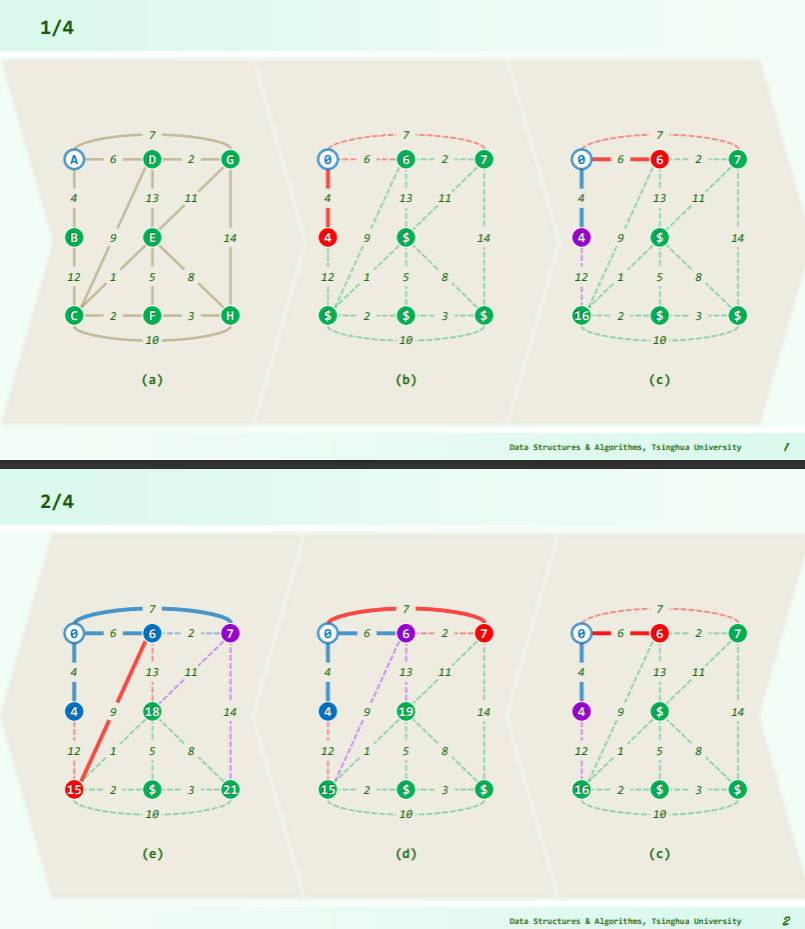
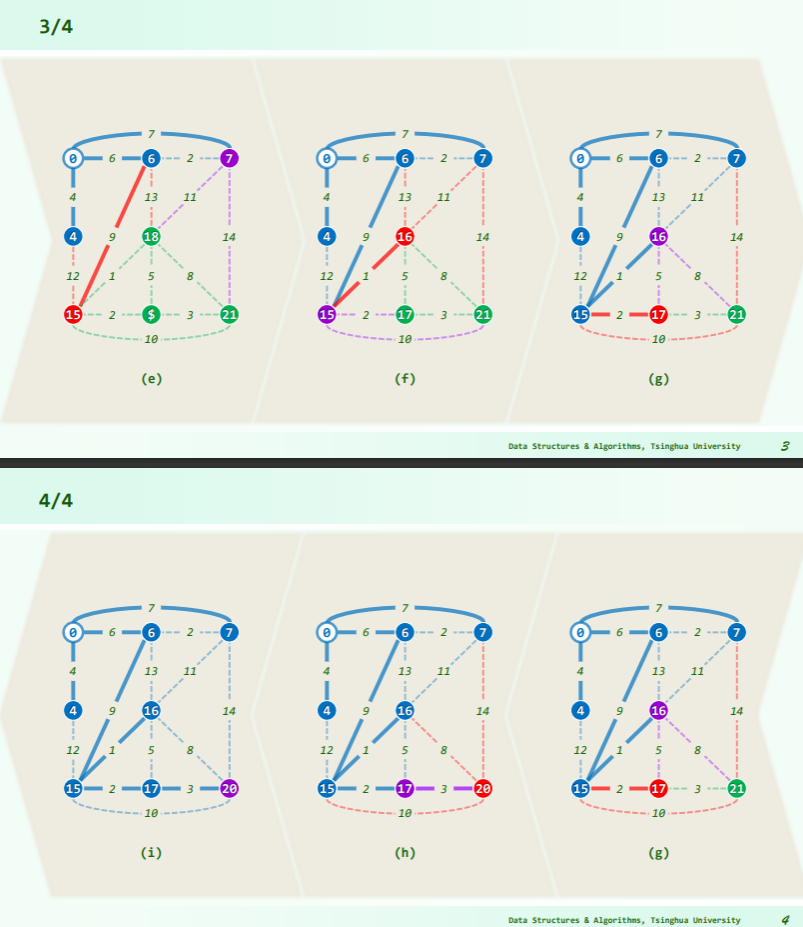
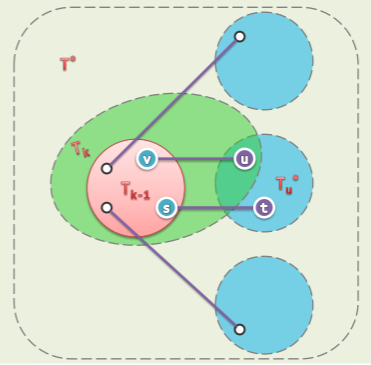
由此，可以得到 Prim 算法的递增式构造方法：

首先，任选： $T_{1} = ({v_{1}}; \emptyset)$
不断地将 $T_{k}$ 扩展为 $T_{k + 1}$ ： $T_{k + 1} = (V_{k + 1}; E_{k + 1}) = (V_{k} \cup {v_{k + 1}}; E_{k} \cup {v_{k + 1}, u})$
由此前的分析，只需将 $(V_{k}; V V_{k})$ 视作原图的一个割，则该割所有跨边中的极短者即是 $(v_{k + 1}, u)$

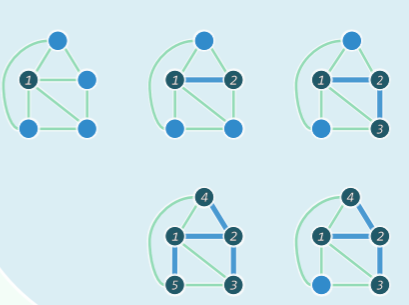
实例

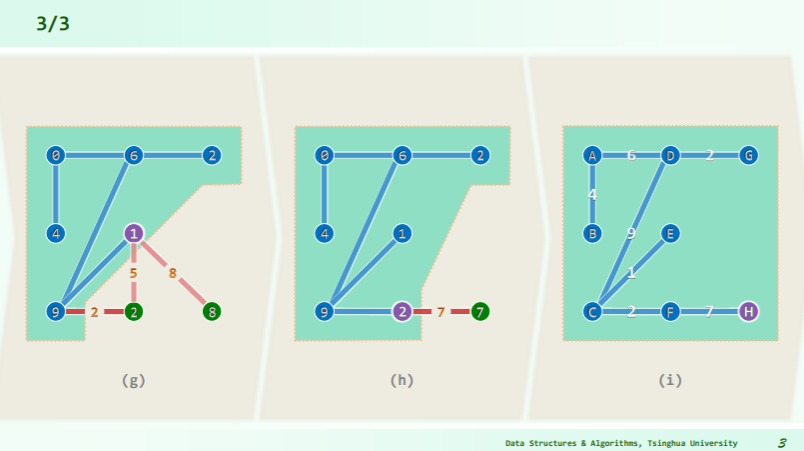
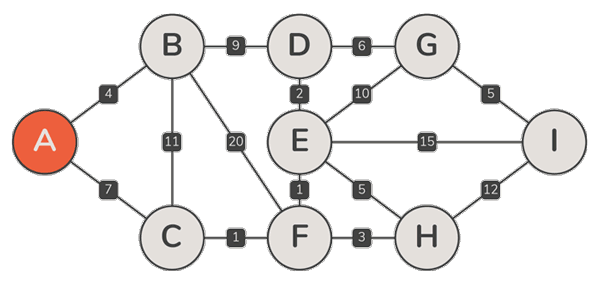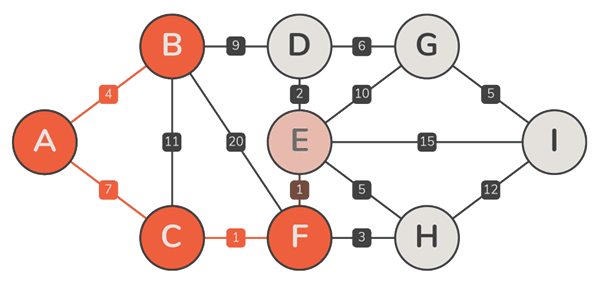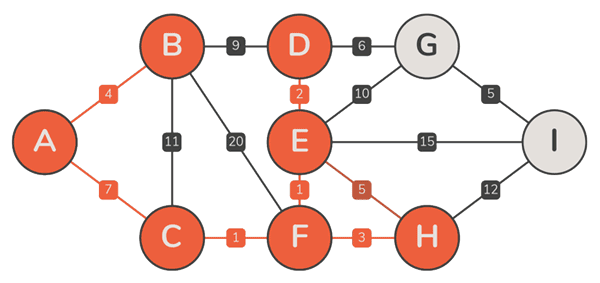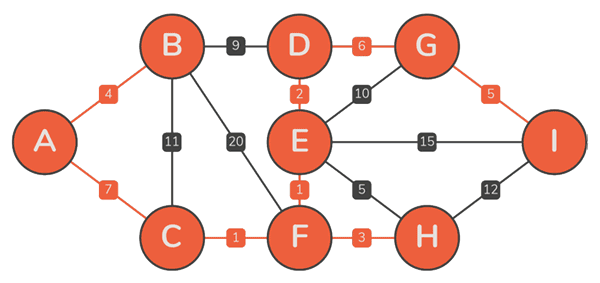
正确性

设 Prim 算法依次选取了边{ e2, e3, …, en }，其中每一条边 ek，的确都属于某棵 MST
但在 MST 不唯一时，由此并不能确认，最终的 T 必是 MST（之一），此时由极短跨边构成的支撑树，未必就是一棵 MST
可行的证明：在不增加总权重的前提下，可以将任一 MST 转换为 T，每一 Tk 都是某棵 MST 的子树，1 ⇐ k ⇐ n —— 6-28题

实现

在图 G 及其子图中，每一轮都为可在一条路径可达的节点标记优先级 priority，其值决定于已确定范围到目标点的距离；
套用 PFS 框架，每一轮 SPT 的增长： $T_{k} \Rightarrow T_{k + 1}$ ，
1. 只需要选出优先级最高的跨边 CROSS及其对应顶点 $u_{k}$ ，
2. 将其接入 $T_{k}$ 即可，随后再更新 $V V_{k + 1}$ 中所有顶点的优先级；
需要注意，优先级随后可能改变（降低）的顶点，必定与 $u_{k}$ 邻接；
因此只需枚举 $u_{k}$ 的每一邻接顶点 $v$ ，并取 $p r i or i t y (v) = min (p r i or i t y (v), ∣∣ u_{k}, v ∣∣)$

因此对应于 Prim 的优先级更新器如下：

template <typename Tv, typename Te> struct PrimPU { //针对Prim算法的顶点优先级更新器
   virtual void operator()( Graph<Tv, Te>* g, Rank v, Rank u ) {
      if ( UNDISCOVERED == g->status( u ) ) //对于v每一尚未被发现的邻接顶点u
         if ( g->priority( u ) > g->weight( v, u ) ) { //按Prim策略做松弛
            g->priority( u ) = g->weight( v, u ); //更新优先级（数）
            g->parent( u ) = v; //更新父节点
         }
   }
};

整体 Prim 算法如下：

template <typename Tv, typename Te> //Prim算法：无向连通图，各边表示为方向互逆、权重相等的一对边
void Graph<Tv, Te>::prim( Rank s ) { // s < n
   reset(); priority ( s ) = 0;
   for ( Rank i = 0; i < n; i++ ) { //共需引入n个顶点和n-1条边
      status( s ) = VISITED;
      if ( -1 != parent( s ) ) type( parent( s ), s ) = TREE; //引入当前的s
      for ( Rank j = firstNbr( s ); - 1 != j; j = nextNbr( s, j ) ) //枚举s的所有邻居j
         if ( ( status( j ) == UNDISCOVERED ) && ( priority( j ) > weight( s, j ) ) ) //对邻接顶点j做松弛
            { priority( j ) = weight( s, j ); parent( j ) = s; } //与Dijkstra算法唯一的不同之处
      int shortest = INT_MAX;
      for ( Rank j = 0; j < n; j++ ) //选出下一极短跨边
         if ( ( status( j ) == UNDISCOVERED ) && ( shortest > priority( j ) ) )
            { shortest = priority( j ); s = j; }
   }
}

Kruskal 算法求 MST

描述

回顾 Prim 算法：

最短边，迟早会被采用
次短边，亦是如此
再次短者，则未必，因为可能出现回路！

Kruskal：贪心原则

根据代价，从小到大依次尝试各边，只要“安全”——次短即可，就加入该边
但是，每步局部最优 = 全局最优？确实，Kruskal 很幸运…

Kruskal 算法：

维护 N 的一个森林：F = (V; E’) ⊆ N = (V; E)
初始化:
- $F = (V; \emptyset)$ 包含 n 棵树（各含 1 个顶点）和 0 条边
- 将所有边按照代价排序
迭代，直到 F 成为1棵树
- 找到当前最廉价的边 e
- 若 e 的顶点来自 F 中不同的树，则
  - 令 E’ = E’ ∪ {e}，然后
  - 将 e 联接的 2 棵树合二为一
整个过程共迭代 n-1次，选出 n-1条边

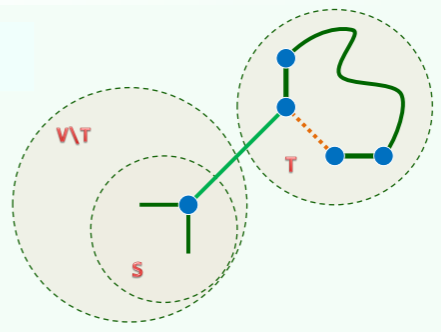
正确性

定理：Kruskal 引入的每条边都属于某棵 MST

设：边 e = (u, v)的引入导致树 T 和 S 的合并
若：将 (T; V\T)视作原网络 N 的割，则：e 当属该割的一条跨边
在确定应引入 e 之前
- 该割的所有跨边都经 Kruskal 考察
- 且只可能因不短于 e 而被淘汰
故：e 当属该割的一条极短跨边
与 Prim 同理，以上论述也不充分，为严格起见，仍需归纳证明：Kruskal 算法过程中不断生长的森林，总是某棵 MST 的子图。

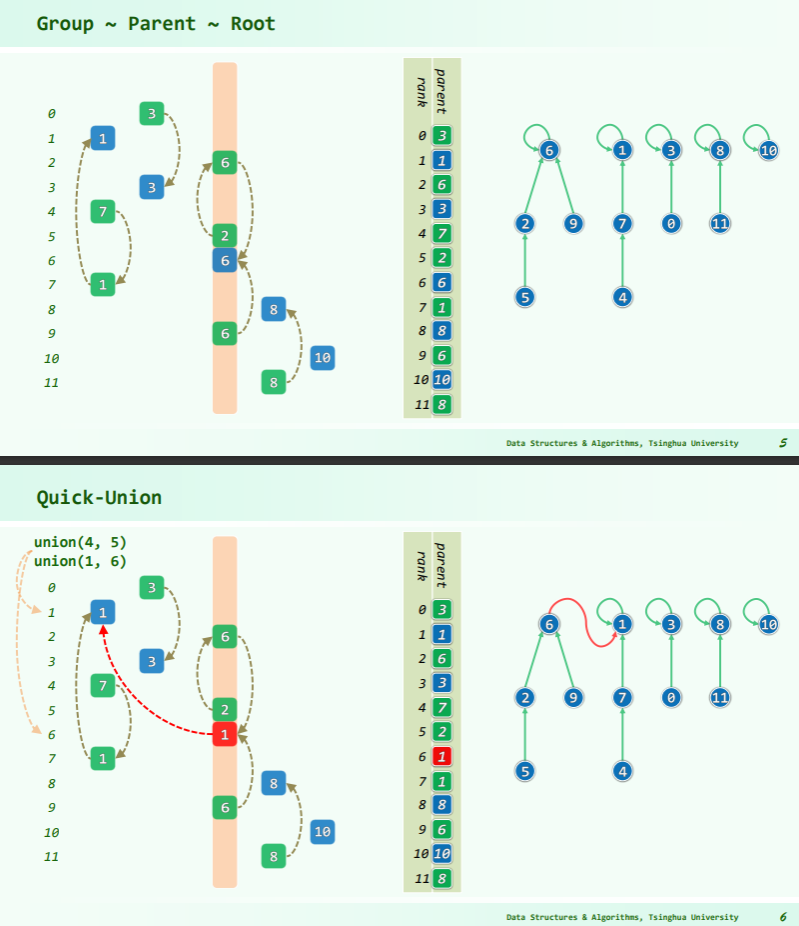
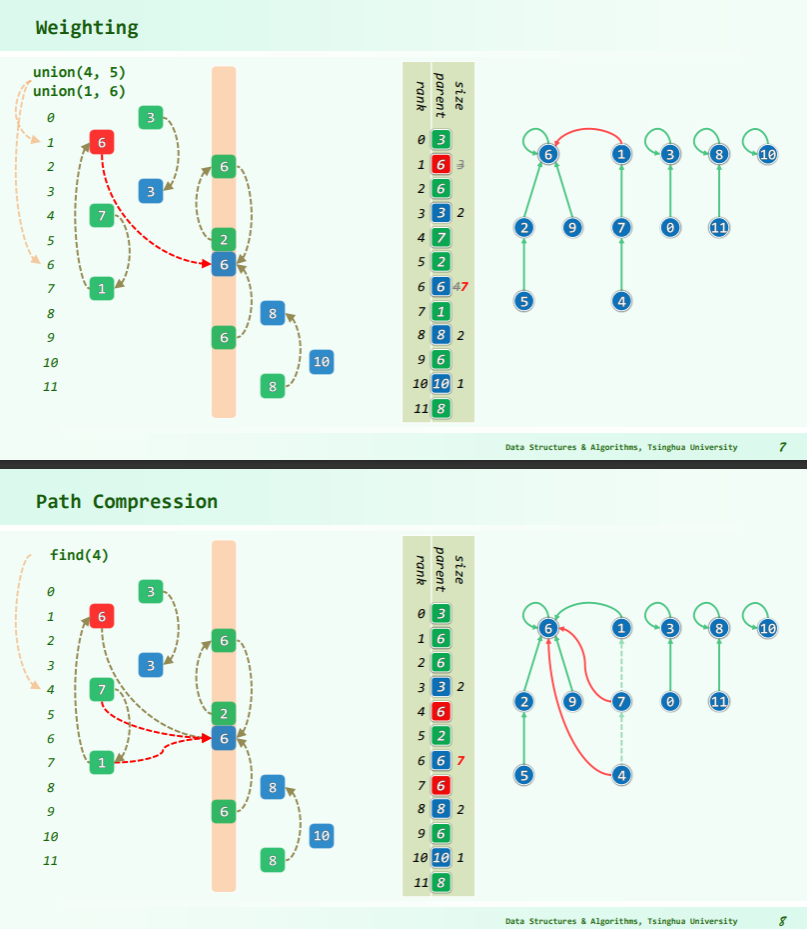
并查集

MST 的 Kruskal 算法

伪代码：
$12345678910 Input. The edges of the graph e, where each element in e is (u, v, w) denoting that there is an edge between u and v weighted w . Output. The edges of the MST of the input graph . Method. res u lt \leftarrow \emptyset sort e into nondecreasing order by weight w for each (u, v, w) in the sorted e if u and v are not connected in the union-find set connect u and v in the union-find set res u lt \leftarrow res u lt ⋃ {(u, v, w)} return res u lt$
算法虽简单，但需要相应的数据结构来支持……具体来说，维护一个森林，查询两个结点是否在同一棵树中，连接两棵树。

抽象一点地说，维护一堆集合，查询两个元素是否属于同一集合，合并两个集合。

其中，查询两点是否连通和连接两点可以使用并查集维护。

如果使用 $O (m lo g m)$ 的排序算法，并且使用 $O (m α (m, n))$ 或 $O (m lo g n)$ 的并查集，就可以得到时间复杂度为 $O (m lo g m)$ 的 Kruskal 算法。

[! note]+ Kruskal 算法的证明思路很简单，为了造出一棵最小生成树，我们从最小边权的边开始，按边权从小到大依次加入，如果某次加边产生了环，就扔掉这条边，直到加入了 n-1 条边，即形成了一棵树。

证明：使用归纳法，证明任何时候 K 算法选择的边集都被某棵 MST 所包含。

基础：对于算法刚开始时，显然成立（最小生成树存在）。

归纳：

假设某时刻成立，当前边集为 F，令 T 为这棵 MST，考虑下一条加入的边 e。

如果 e 属于 T，那么成立。

否则，T+e 一定存在一个环，考虑这个环上不属于 F 的另一条边 f（一定只有一条）。

首先，f 的权值一定不会比 e 小，不然 f 会在 e 之前被选取。

然后，f 的权值一定不会比 e 大，不然 T+e-f 就是一棵比 T 还优的生成树了。

所以，T+e-f 包含了 F，并且也是一棵最小生成树，归纳成立。

Footnotes

Gabow, H. N., & Tarjan, R. E. (1985). A Linear-Time Algorithm for a Special Case of Disjoint Set Union. JOURNAL OF COMPUTER AND SYSTEM SCIENCES, 30, 209-221. PDF

↩

Tarjan, R. E., & Van Leeuwen, J. (1984). Worst-case analysis of set union algorithms. Journal of the ACM (JACM), 31(2), 245-281.ResearchGate PDF ↩

Yao, A. C. (1985). On the expected performance of path compression algorithms.SIAM Journal on Computing, 14(1), 129-133. ↩

指向原始笔记的链接

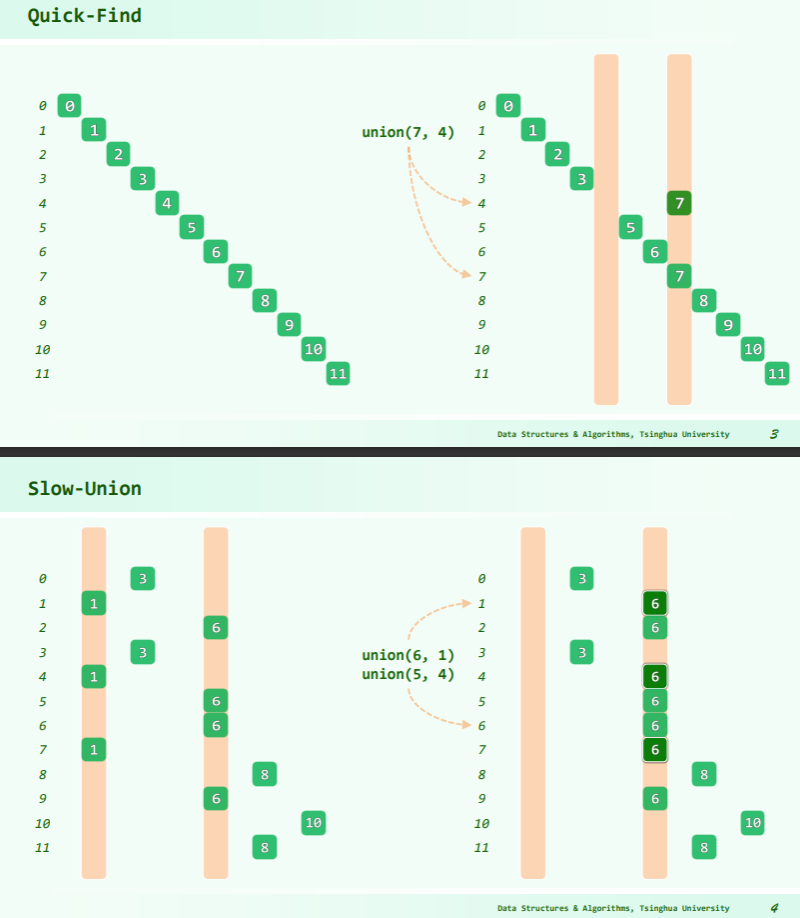
//Quick-Find(就是启发式合并)
class UnionFind:
	def __init__(self, n): #group[]记录各元素所属子集；初始各成一类，以[0,n)间整数标识
		self.g = self.n = n; self.group = [ k for k in range(n) ]
	def find(self, k):
		return self.group[k]
	def union(self, i, j):
		iGroup , jGroup = self.group[i] , self.group[j]
		if iGroup == jGroup: return
		for k in range(self.n):
			if (self.group[k] == jGroup): self.group[k] = iGroup
		self.g -= 1

Floyd-Warshall 算法求 SPT

直觉：依次将各顶点作为源点，调用 Dijkstra 算法，其时间复杂度 = $n \times O (n^{2}) = O (n^{3})$ —— 可否更快？

思路：图矩阵 ⇒ 最短路径矩阵效率： O(n^3)，与执行 n 次 Dijkstra 相同 —— 既如此，F.W.之价值何在？优点：形式简单、算法紧凑、便于实现；允许负权边（尽管仍不能有负权环路） Floyd-Warshall 算法

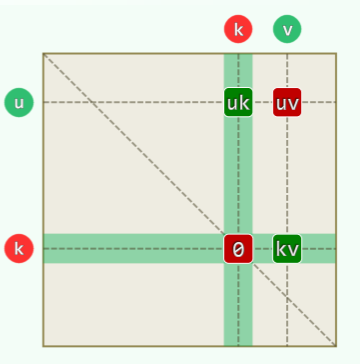
问题描述

u 和 v 之间的最短路径可能是

不存在通路，或者
直接连接，或者
最短路径 (u, x) + 最短路径 (x, v)

将所有顶点随意编号：1, 2, …, n 。定义： $d^{k} (u, v) =$ 中途只经过前 k 个顶点中转，从 u 通往 v 的最短路径长度：

$d^{k} (u, v) = w (u, v), (i f k = 0)$
$d^{k} (u, v) = min {d^{k - 1} (u, v), d^{k - 1} (u, k) + d^{k - 1} (k, v)}, (i f k \geq 1)$

蛮力递归

weight dist( node * u, node * v, int k )
	if ( k < 1 ) return w( u, v );
	u2v = dist( u, v, k-1 ); //经前k-1个点中转
	for each node x  { u, v } //x作为第k个可中转点
		u2x2v = dist( u, x, k-1 ) + dist( x, v, k-1 ); //递归
		u2v = min( u2v, u2x2v ); //择优
	return u2v;

动态规划

for k in range(0, n)
	for u in range(0, n)
		for v in range(0, n)
			A[u][v] = min( A[u][v], A[u][k] + A[k][v] )

蛮力递归会存在大量重复的递归调用，可以使用动态规划记忆化：维护一张表，记录需要反复计算的数值：

去掉其中所有边能使一张网络流图不再连通（即分成两个子图）的“边集”称为图的割（英语：cut） ↩

🌰Senjl's Digital Garden🐉

Recent writing

Welcome to Senj's Digital Garden

4-地址空间

5-进程

探索

81-Graph-Application

拓扑排序

DAG

拓扑排序的要求

DAG 中的偏序关系

零入度

思路

策略（伪代码）

实例

零出度

思路

策略（描述）

实例

代码

双连通分量

判定

定义

暴力法

改进：利用 DFS

代码

复杂度

实例

优先级搜索

算法框架

复杂度

Dijkstra 算法求最短路径

问题描述

最短路径树

算法

实例

实现

Prim 算法求 MST

MST 是什么

MST != SPT

蛮力算法

改进思路：极短跨边

实例

正确性

实现

Kruskal 算法求 MST

描述

Kruskal 算法：

正确性

并查集

MST 的 Kruskal 算法

Footnotes

Floyd-Warshall 算法求 SPT

问题描述

蛮力递归

动态规划

Footnotes

关系图谱

目录

反向链接