E0-Regularization

Regularized Hypothesis Set

由前文论述，过拟合的一个原因就是假设集 $\mathcal{H}$ 过于复杂，那么如果能将复杂的假设集退化到简单的假设集，不就可以降低过拟合程度吗？——这就是正则化！

• 
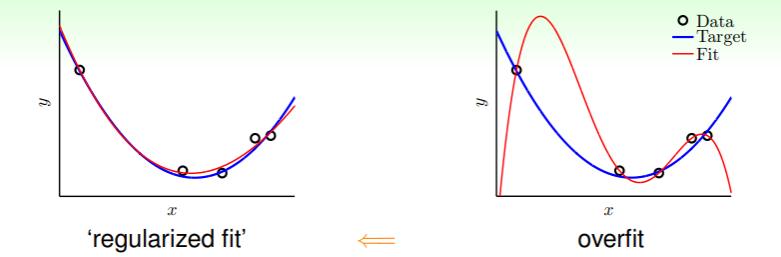
• 我们以十阶假设集 ${\mathcal{H}}_{10}$ 和二阶假设集 ${\mathcal{H}}_2$ 为例，它们各自可以表示为 $w_0+w_{1}x+w_2{x}^2+w_3{x}^3+...+w_{10}{x}^{10}$ 和 $w_0+w_{1}x+w_2{x}^2$ ，因此 ${\mathcal{H}}_2$ 就是 ${\mathcal{H}}_{10}$ 加上一些限制：$w_3=w_4=...=w_{10}=0$ —— “退化”其实就是“限制”

Steps of Constraint

现在来看看具体如何限制：

• 对于 Regression 算法，在两个不同假设空间的假设与错误评估函数可以如下设置：
• 既如此，我们不妨直接使用 ${\mathcal{H}}_2$ 中的假设，并且可以进一步放宽限制，不是必须 $w_3=w_4=...=w_{10}$ 这八个权重为 0 ，而是 $w_0,w_1,...,w_{10}$ 中任意八个权重为 0 ： 这样的好处是 ${\mathcal{H}}_2^{\prime }$ 不仅比 ${\mathcal{H}}_2$ 更加灵活，但相对 ${\mathcal{H}}_{10}$ 发生 overfit 的风险又更低；不过坏消息是要从 ${\mathcal{H}}_2^{\prime }$ 中挑选出最佳的假设，时间复杂度是 NP-hard 的；
• 进一步思考，${\mathcal{H}}_2^{\prime }$ 的权重向量是稀疏的（sparse），因此不妨考虑权重向量的欧氏距离，如果其欧氏距离小于一个常数，就认定其满足了对高维假设集的限制：
  • 考查 $\mathcal{H}(C)$，它其实与 ${\mathcal{H}}_2^{\prime }$ 有一定重叠，但又不完全相同，
  • 并且随着 C 的增大，有这样的关系：$\mathcal{H}(0)\subset \mathcal{H}(1.126)\subset ...\subset \mathcal{H}(1126)\subset ...\subset \mathcal{H}(\infty )={\mathcal{H}}_{10}$ ，在假设集 $\mathcal{H}(C)$ 中最佳的假设称为正则化的假设 ${\mathbf{w}}_{REG}$ ，其选取的复杂度为 $\mathcal{O}(N)$；

Name history of Regularization

正则化（Regularization）在机器学习中的命名来源与其在数学和统计学中的应用有关。在更广泛的背景下，正则化是解决病态问题（ill-posed problems）或防止过拟合（overfitting）的一种方法。这个概念在数学、统计学、计算机科学等多个领域都有应用，尤其在机器学习中扮演着重要角色。

1. 病态问题（Ill-posed problems） 在数学和统计学中，一个问题被认为是“病态的”（ill-posed），如果它不满足所谓的哈达马条件（Hadamard conditions），这些条件通常包括：

• 解的存在性：问题必须有解。

• 解的唯一性：问题的解必须是唯一的。

• 解的稳定性：解对于初始条件的小变化是连续的或稳定的。 如果一个问题不满足这些条件之一，那么它可能很难解决或者解决方案可能不可靠。例如，在逆问题（inverse problems）中，这些条件往往不被满足，导致解决这类问题变得复杂。

2. 正则化的作用 在面对病态问题时，正则化的主要目的是使问题变得更加“良态”（well-posed）。通过引入额外的信息或约束（例如惩罚项），可以帮助稳定解的计算，保证解的唯一性或连续性。在机器学习中，这通常意味着在模型复杂度和训练数据拟合之间寻找平衡，防止模型过于复杂而导致的过拟合。

3. 在机器学习中的应用 在机器学习中，正则化通过在损失函数中添加一个额外的项（例如 L1 或 L2 惩罚项）来实现。这个额外的项惩罚模型的复杂度，通常与模型参数的大小成正比。通过这种方式，正则化鼓励模型学习更简单、更泛化的模式，而不是复杂且可能仅适用于训练数据的模式。

练习：理解 $\mathcal{H}(C)$

Weight Decay Regularization

那么如何从 $\mathcal{H}(C)$ 中选取最佳的假设 ${\mathbf{w}}_{REG}$ 呢？和之前一样，我们要考虑使 $E_{in}$ 最小的假设，写成矩阵和向量运算的形式如下：

$$\underset{\mathbf{w}\in {\mathbb{R}}^{Q+1}}{\min }{E}_{in}(\mathbf{w})=\frac{1}{N}\underset{(Z\mathbf{w}-\mathbf{y}{)}^T(Z\mathbf{w}-\mathbf{y})}{\underbrace{\sum _{n=1}^N({\mathbf{w}}^T{\mathbf{z}}_n-y_n{)}^2}},\text{ subject to }\underset{{\mathbf{w}}^T\mathbf{w}}{\underbrace{\sum _{q=0}^Q{\mathbf{w}}_q^2}}\le C$$

这里 $({\mathbf{w}}^T{\mathbf{z}}_n-y_n{)}^2$ 项可以写成向量内积的形式：$(\mathrm{Z}\mathbf{w}-\mathbf{y}{)}^{\mathrm{T}}(\mathrm{Z}\mathbf{w}-\mathbf{y})$ ，并且 ${\mathbf{w}}^T\mathbf{w}\le C$ 的含义是最佳的 ${\mathbf{w}}_{REG}$ 可选范围是在半径为 $\sqrt{C}$ 的（超）球体内（hypersphere）。

Calculate the minimum $E_{in}$: Lagrange Multiplier

回想多元函数有约束极值问题的拉格朗日乘数法，我们这里要求 $\underset{\mathbf{w}\in {\mathbb{R}}^{Q+1}}{\min }{E}_{in}(\mathbf{w})=\frac{1}{N}(Z\mathbf{w}-\mathbf{y}{)}^T(Z\mathbf{w}-\mathbf{y})\text{ s.t. }{\mathbf{w}}^T\mathbf{w}\le C$ ，也要用到这个方法：

• 
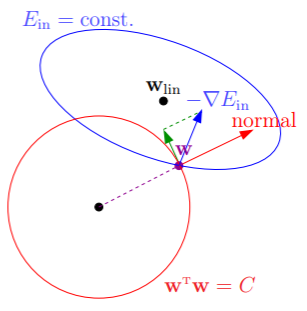
• 上图中，$E_{in}(\mathbf{w})$ 下降的方向是梯度的反方向 $-\nabla E_{in}(\mathbf{w})$ ，并且如果没有限制的话，会一直下降到线性回归问题里探讨过的 ${\mathbf{w}}_{LIN}$ ，
• 然而 ${\mathbf{w}}_{REG}$ 可选的范围不超过半径为 $\sqrt{C}$ 的圆，因此 ${\mathbf{w}}_{REG}$ 大多情况时在圆的边界上，那么如何判断边界上一点是否已经是最小的呢？我们选取该点处切平面的法向量为 $\mathbf{w}$ ，因此如果该点处梯度的反方向 $-\nabla E_{in}(\mathbf{w})$ 不与 $\mathbf{w}$ 向量平行——即有沿着垂直于 $\mathbf{w}$ 方向的分量，那么就可以不断地降低 $E_{in}$ 而又不超过限制，
• 因此，当 $E_{in}$ 一直降低到最小，那么就代表着此处梯度的反方向与 $\mathbf{w}$ 平行，即梯度 $-\nabla E_{in}({\mathbf{w}}_{REG})$ 与最佳的 ${\mathbf{w}}_{REG}$ 成正比：$-\nabla E_{in}(\mathbf{w})\propto {\mathbf{w}}_{REG}$ ，我们由拉格朗日乘数法，就是要找到 $\lambda$ 满足 $\nabla E_{in}(\mathbf{w})+\frac{2\lambda }{N}{\mathbf{w}}_{REG}=0$ ，
• 我们不妨设 $\lambda >0$，在 线性回归问题 中我们也曾探讨过 $\nabla E_{in}(\mathbf{w})$ 的结果，因此解上面的式子相当于解 $\frac{2}{\mathrm{N}}({\mathrm{Z}}^{\mathrm{T}}\mathrm{Z}{\mathbf{w}}_{\mathrm{REG}}-{\mathrm{Z}}^{\mathrm{T}}\mathbf{y})+\frac{2\lambda }{\mathrm{N}}{\mathbf{w}}_{\mathrm{REG}}=0$ ，则得到 ${\mathbf{w}}_{REG}\leftarrow ({\mathrm{Z}}^{\mathrm{T}}\mathrm{Z}+\lambda \mathrm{I}{)}^{-1}{\mathrm{Z}}^{\mathrm{T}}\mathbf{y}$ ；
  • $({\mathrm{Z}}^{\mathrm{T}}\mathrm{Z}+\lambda \mathrm{I})$ 这个矩阵一定是可逆的，因为 ${\mathrm{Z}}^{\mathrm{T}}\mathrm{Z}$ 是半正定的，加上一个正的单位矩阵，必然是正定的，因此也必然可逆，
  • 在统计学中，$({\mathrm{Z}}^{\mathrm{T}}\mathrm{Z}+\lambda \mathrm{I}{)}^{-1}{\mathrm{Z}}^{\mathrm{T}}\mathbf{y}$ 也称为 ridge regression ；

Calculate the Minimum $E_{in}$: Transform to Constraintless

或者，从另一个角度来看，要使得 $\nabla E_{in}(\mathbf{w})+\frac{2\lambda }{N}{\mathbf{w}}_{REG}=0$ ，等价于使 $\underset{E_{aug}(\mathbf{w})}{\underbrace{E_{in}(\mathbf{w})+\frac{\lambda }{N}{\mathbf{w}}^T\mathbf{w}}}$ 取得最小（对原式做积分），其中 ${\mathbf{w}}^T\mathbf{w}$ 称为 regularizer ，而整个式子称为 augemented error —— $E_{aug}(\mathbf{w})$ 。

如此，实现了化受限为不受限，因此使得 $E_{aug}$ 最小的 $\mathbf{w}$ 就是受限问题中要求的 ${\mathbf{w}}_{REG}$ ：${\mathbf{w}}_{REG}\leftarrow arg\underset{\mathbf{w}}{\min }{E}_{aug}(\mathbf{w})$ 。

How $\lambda$ Affect？

从上面的论证也可以看出，$\lambda$ 的作用与限制 $C$ 是一致的，因此我们可以直接探讨 $\lambda$ 大小的影响。那么 $\lambda$ 对拟合程度的影响究竟是什么呢？

• 
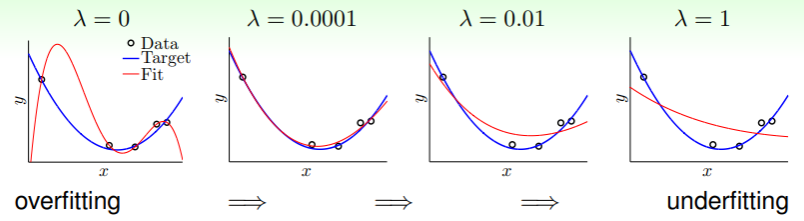
• $\lambda =0$ 相当于没有做任何约束，即没有任何正则化的要求；而随着 $\lambda$ 的增大，约束逐渐增强，越大的 $\lambda$ 等同于越短的 $\mathbf{w}$ ，也就是越小的 $C$ ；
• 不过当 $\lambda$ 过大时，也会导致得到的假设与目标函数偏离变大，也就是 underfitting ；
• 这就是正则化的哲学：a little regularization goes a long way!
• 我们称 $E_{aug}$ 中 $\frac{\lambda }{N}{\mathbf{w}}^T\mathbf{w}$ 这一项为 weight-decay regularization ；

Legendre Polynomials

在实现维度之间的转换时，我们需要使用转换函数 $\Phi$ ，我们知道它是一个多项式函数，因此设置为 $\Phi (\mathbf{x})=(1,x,x^2,...,x^Q)$ 。不过这样的函数有一些问题，比如在特征向量 $\mathbf{x}$ 中所有维的取值都在 $[-1,+1]$ 区间内时，高维的部分将会变得很小，因此其对应的权重就会变得很大，而我们又要求权重不应超过某个限制，因此这代表着对高维的惩罚较大，这并不公平。

这个问题的关键就是因为这 $Q+1$ 个坐标不是垂直的，导致对低维的容忍度比较高，而对高维的惩罚比较大，因此我们应当做一些坐标转换——在多项式的空间里找出一些垂直的基底，各基底的内积为 0 ，正交化的转换函数记作 $(1,L_1(x),L_2(x),...,L_Q(x))$ ，称为 Legendre Polynomials ：

• 

练习：${\mathbf{w}}_{REG}$ 与 ${\mathbf{w}}_{LIN}$ 的联系

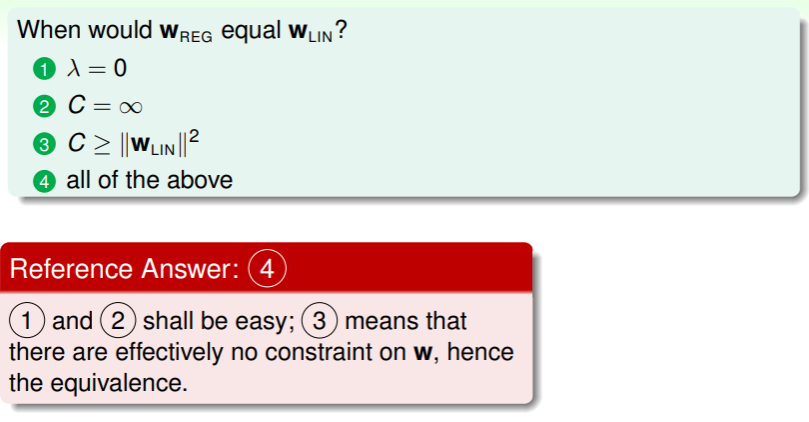
• 第三个式子在几何意义上就是限制把最佳解包围在内；

Regularization and VC Theory

$E_{aug}$ Vs. VC Bound Guarantee

我们前面提到正则化就是使 $E_{in}$ 受到某种限制：

$$\underset{\mathbf{w}}{\min }{E}_{in}(\mathbf{w})\text{ s.t. }{\mathbf{w}}^T\mathbf{w}\le C$$

，这种限制等价于使 $E_{aug}$ 最小化：

$$\underset{\mathbf{w}}{\min }{E}_{aug}(\mathbf{w})=E_{in}(\mathbf{w})+\frac{\lambda }{N}{\mathbf{w}}^T\mathbf{w}$$

，联系之前所学的 VC 理论 ，其中也相当于对 $E_{in}$ 做出了一些限制：

$$E_{out}(\mathbf{w})\le E_{in}(\mathbf{w})+\Omega (\mathcal{H}(C))$$

。因此类比，最小化 $E_{aug}$ 的过程似乎就是间接地获取没有 $\mathcal{H}(C)$ 限制的 VC bound 的保证的过程。

详细地对比 $E_{aug}$ 和 VC bound ：

• $E_{aug}$ 中称为 regularizer 的 ${\mathbf{w}}^T\mathbf{w}$ 项，含义是一个假设的复杂度，其值越大，代表假设的维数越高，假设越复杂；不妨记作 $\Omega (\mathbf{w})$ ，
• VC bound 中 $\Omega (\mathcal{H})$ 项是对一个假设集的复杂度的评估；
• 因此如果 $\frac{\lambda }{N}\Omega (\mathbf{w})$ 能够对 $\Omega (\mathcal{H})$ 做出合理的代表，那么就可以认为 $E_{aug}$ 可以在一定程度上代表 $E_{out}$，并且比 $E_{in}$ 更加精确。

因此从 VC dimension 的角度来仔细查看 $E_{aug}$ 的计算公式：

$$\underset{\mathbf{w}\in {\mathbb{R}}^{\tilde{d}+1}}{\min }{E}_{aug}(\mathbf{w})=E_{in}(\mathbf{w})+\frac{\lambda }{N}\Omega (\mathbf{w})$$

• 这个模型中复杂度为 $d_{VC}(\mathcal{H})=\tilde{d}+1$ ，这是因为在最小化的过程中要考虑到所有样本 $\mathbf{w}$ ，
• 但是由于限制 $\mathcal{H}(C)$ 的存在，并不是所有 $\mathbf{w}$ 都会用到，因此我们称在限制存在的条件下的 VC dimension 为 effective VC dimension ：$d_{EFF}(\mathcal{H},\underset{\min E_{aug}}{\underbrace{\mathcal{A}}})$ ，
• 这意味着尽管 $d_{VC}(\mathcal{H})$ 可能很大，但对学习算法 $\mathcal{A}$ 进行正则化后，有效 VC dimension 可能非常小。

练习：理解有效 VC dimension

General Regularizers

为了推广正则化，我们需要尝试提出应对不同场景的正则化方式：

1. target-dependent：在预先知道目标函数或其部分特征时，我们可以利用这些特征进行正则化：比如如果我们预知目标函数是一个偶函数，那么就可以使奇次项的权重全都变小；
2. plausible：在希望目标函数平滑、简单时，可以使用 sparsity (L1) regularizer
3. friendly：在希望目标函数容易优化时，可以使用 weight-decay (L2) regularizer
4. 除此之外，如果我们不能确定正则化后的结果是否变得更好，那还有 $\lambda$ 把关，只要其为 0 ，就相当于没有进行正则化。

因此，更加一般的，$\text{augmented error}=\text{error }\widehat{\text{err}}+\text{regularizer }\Omega$ 。

L1&L2 Regularizer

L2 Regularizer 是我们之前谈到的通过拉格朗日乘数法可以很快实现找到最优 ${\mathbf{w}}_{REG}$ 的正则化方式：

• 
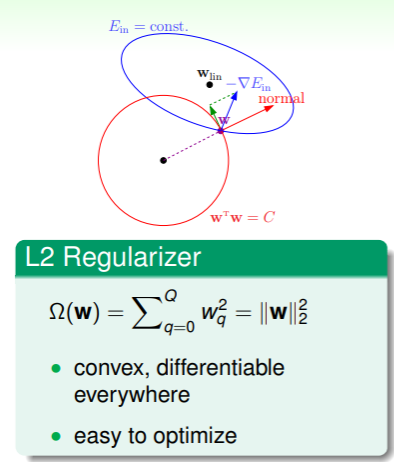
• 其中对 $\mathbf{w}$ 来说，在任何地方都是凸的、可微的；

而 L1 Regularizer 是 one-norm 的，具体形式是绝对值函数：

• 
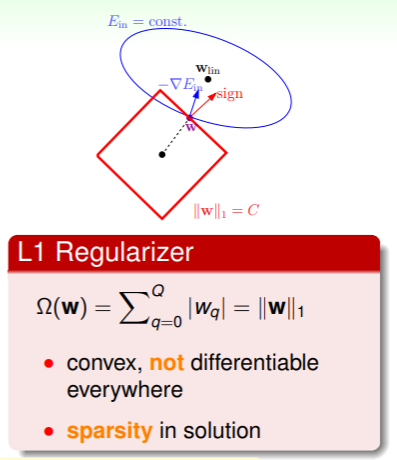
• 这时对 $\mathbf{w}$ 来说虽然是凸的，但在某些地方不再可微，虽然解起来麻烦一些，不过原理还是拉格朗日乘数法，只要 $-\nabla E_{in}$ 不与当前点的法方向平行，那就可以继续下降；
• 总之，L1 Regularizer 的解通常位于顶点上，此处 $\mathbf{w}$ 的部分维将会是 0 ，因此可以成为稀疏的（sparse），因此 L1 Regularizer 通常认为是计算起来简单的。

什么是 one-norm ？

• Norm (mathematics) - Wikipedia

Noise and $\lambda$

噪音的存在会使得正则化的过程中不再平滑、可微，那么具体的影响是什么呢？

• 
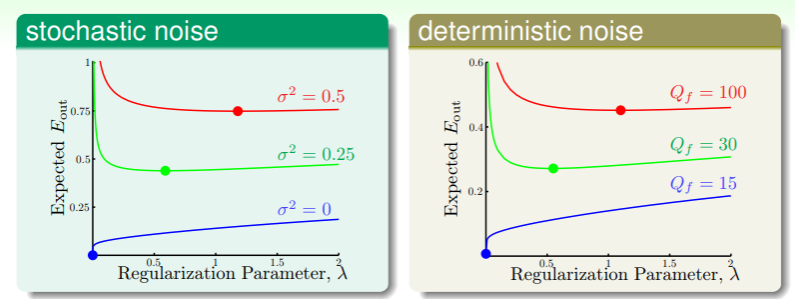
• 上图表明，噪音强度越大，就越需要正则化，就像在越颠簸的路段上行车越需要不停地点踩刹车；
• 但是噪音强度我们事先无法确定，因此选择合适的正则化方式尤为重要，这就涉及到下一章的内容——验证。

练习：选择最合适的正则化方式

• 这里的正则化方式 $\Omega (\mathbf{w})$ 使用了 Legendre polynomial 多项式，在高维时惩罚较大，因此适合使用于低维的假设集；