40-Feasibility-of-Learning

Learning 究竟是否可行？如何判断？

Learning is Impossible?

机器学习的反对者通常认为模型都是基于已知预测未知，而如此必然会出错，因此 Learning 是不可能成立的，例如下面两个例子：

1. 对于预测这个新图形的输出结果，不论+1 或-1 都可以反驳，因此完全可以唱反调——无论回答什么都是错误的：
2. 对于预测一个 3bit 的向量所对应的输出，一共有 $2^3=8$ 的空间，若已知 5 个样本，对剩余三种样本进行预测，则会产生 $2^3=8$ 个可行的 f ，那么根据 $\mathcal{D}$ 进行推演的 g 无论选择什么，都必然不会完全正确：
   • “天下没有免费的午餐”是对这个案例的最好概括——预测必然基于过去而面向未来，过去是确定的，未来是不确定的，想要得到确定的未来，必然要付出某种代价；
   • 事实上，犯错是必然的，但也正是我们所需要的，只有接纳某些犯错，才会获得有价值的结果。

练习：没有免费的午餐

Probability to the Rescue

但机器学习实际的目标是以尽可能低的代价容忍犯错，从而获得尽可能有效的结果以指导后续的预测、估计等行为。例如数理统计中的一个经典问题，如何从无穷多个二色球的罐子里，估计不同颜色小球的比例？

• 
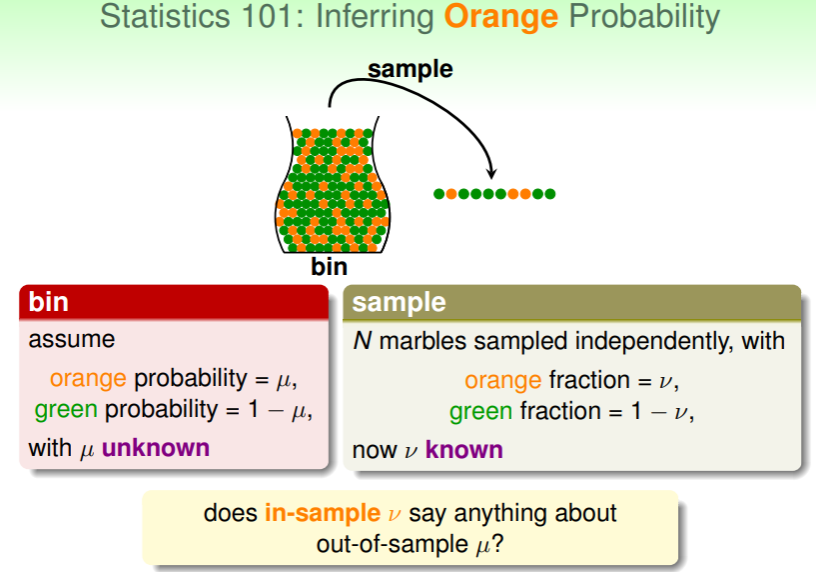
• 若假定罐子里橙色小球的比例为 $\mu$ ，而这个比例是未知的；我们能做的仅是从罐子里取出一定数量的样本，根据样本中橙色小球的比例 $\upsilon$ 来估计 $\mu$ ；
• $\text{Possible}\ne \text{Probable}$ ：样本的比例 $\upsilon$ 当然不能完全代表罐子中的实际比例 $\mu$，但是却能够以某种概率尽可能接近地估计 $\mu$ —— Hoeffding’s Inequality!

Hoeffding’s Inequality

Hoeffding’s Inequality 的形式为：

$$\text{Prob}[|\upsilon -\mu |>ϵ]\le 2e^{-2{ϵ}^{2}N}$$

其含义是：在抽取样本的数量 N 极大时，$\upsilon$ 收敛于 $\mu$ ，换言之，$\upsilon =\mu$ 这个判断是 probably approximately correct (PAC) 的。

因此回到估计橙色小球比例的问题：

• N 的数量越大，就能以越小的差距 $ϵ$ 获得对 $\mu$ 的合理估计 $\upsilon$ ：

Different between Hoeffding's and Chebyshev's

Hoeffding’s Inequality 和 Chebyshev’s Inequality 都是概率论中用来估计随机变量偏离其期望值的概率的不等式，但它们有一些关键的区别和联系：

1. 适用范围:

• Hoeffding’s Inequality：专门用于有界随机变量。它提供了一个概率上限，用于衡量独立随机变量之和偏离其期望值的程度。这个不等式对于任何有界的随机变量都有效，无论其分布如何。
• Chebyshev’s Inequality：适用于任意分布的随机变量，只要其期望值和方差是有定义的。这个不等式不要求随机变量是有界的，但需要已知其方差。

2. 形式和精确度:

• Hoeffding’s Inequality：通常提供一个更紧的（即更小的）概率上限，特别是对于有界变量。它对于样本量的增加非常敏感，可以有效利用这一信息。
• Chebyshev’s Inequality：通常不如 Hoeffding’s Inequality 紧密，特别是对于有界变量。但是，它的优势在于适用于更广泛的情况，尤其是当关于随机变量分布的信息很少时。

3. 数学表达式:

• Hoeffding’s Inequality：对于独立的有界随机变量 $X_1,X_2,\dots ,X_n$，其和 $S_n=\sum _{i=1}^n{X}_i$ 与其期望值 $E[S_n]$ 的偏差被给定概率界限所限制。
• Chebyshev’s Inequality：对于任意随机变量 $X$，其值与其期望值 $\mu =E[X]$ 的偏差超过 $k$ 个标准差的概率被限制为 $1/k^2$。

总的来说，这两个不等式都是处理随机变量偏离其期望值的强大工具，但它们各自在不同的情境下更为适用。Hoeffding’s Inequality 在处理有界变量时特别有用，而 Chebyshev’s Inequality 在对随机变量的分布信息较少时更加通用。

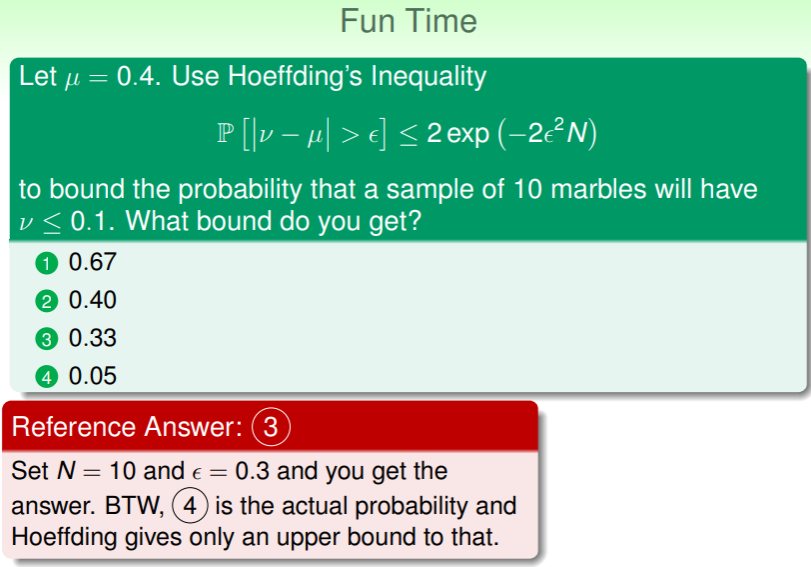
练习：利用 Hoeffding

• $\frac{2}{e^{1.8}}=0.3305978$

Connection to Learning

From Probability to ML

那么，如何从上述的概率统计推演到机器学习呢？

• 
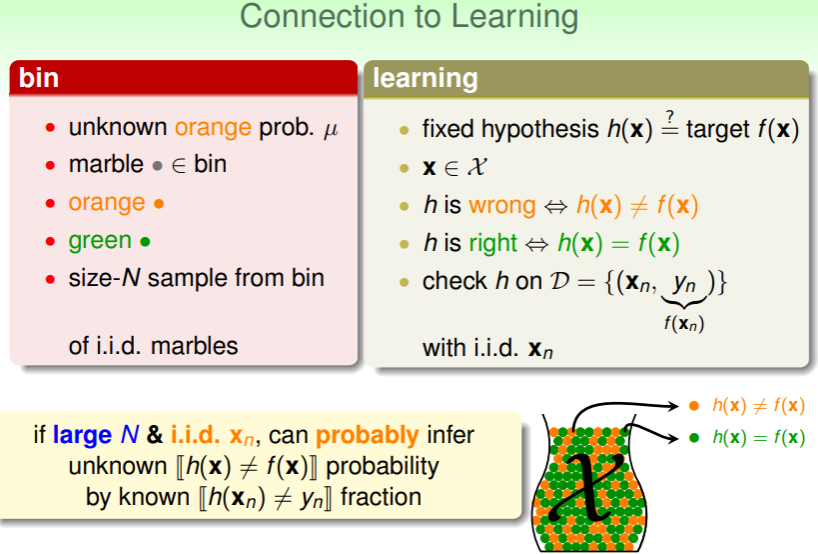
• 罐子中我们具体的问题或信息是橙色小球的比例 $\mu$ 和抽样样本的数量 N ，抽象为 learning ，我们可以提出一个假设函数 $h(\mathbf{x}),\mathbf{x}\in \mathcal{X}$ 来估计能给出正确判断的目标函数 $f(\mathbf{x})$，
• 对每个样本 $\mathbf{x}$ ，假设 $h$ 能够正确实现估计 $⟺h(\mathbf{x})=f(\mathbf{x})$，那么在抽样样本集 $\mathcal{D}=\{({\mathbf{x}}_n,y_n)\}$ 上检查 $h({\mathbf{x}}_n)=f({\mathbf{x}}_n)$ 的比例（即，正确率），则可以从该比例推断在完整数据集（即罐子里）$h(\mathbf{x})=f(\mathbf{x})$ 是正确的概率；

$E_{in}$ and $E_{out}$

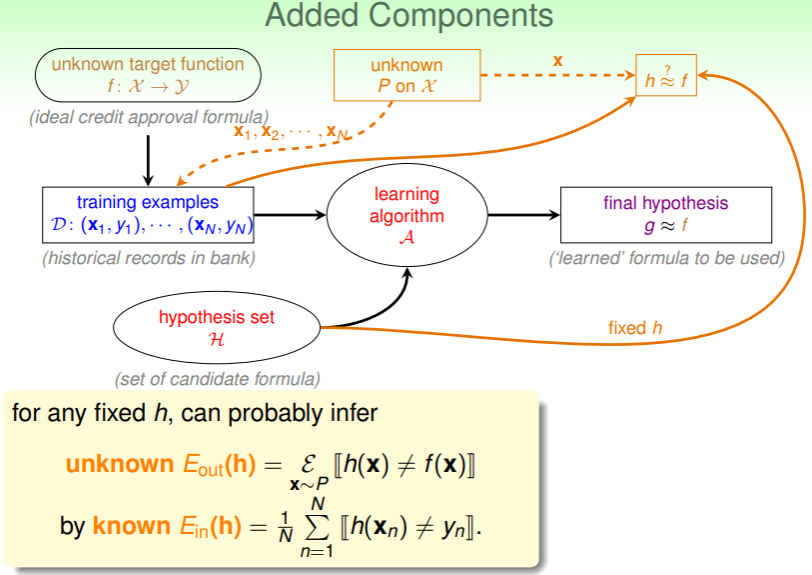
从而，我们可以如下完善 Machine Learning 的流程图：

• 

对于任意同一个假设 $h$ ，我们都可以从已知的训练集中犯错的比例：

$$E_{in}(h)=\frac{1}{N}\sum _{n=1}^N[h({\mathbf{x}}_n)\ne y_n)]$$

估计全局中 $h$ 对 $f$ 的估计的犯错率：

$$E_{out}(h)=\underset{\mathbf{x}\sim P}{\mathbb{E}}[h(\mathbf{x})\ne f(\mathbf{x})]$$

，这里 $E_{out}$ 是对服从特定分布的样本 $\mathbf{x}\sim P$ 中假设与目标不同的期望。

同样，Hoeffding’s Inequality 也可以用于这两种犯错概率的估计：

$$\text{Prob}[|E_{in}(h)-E_{out}(h)|>ϵ]\le 2e^{-2{ϵ}^{2}N}$$

，这意味着对于任意的 N 和 $ϵ$ 都能推导出犯错率的上界，而不必知道确切的 $E_{out}(h)$ ，即 $f$ 和 橙色小球的比例 $P$ 仍然是未知的，$E_{in}(h)=E_{out}(h)$ 是 probably approximately correct 的；

从而，如果 $E_{in}(h)\approx E_{out}(h)$ 且 $E_{in}(h)$ 相当小，我们也可以认为 $E_{out}(h)$ 也足够小，此时 $h$ 可以作为 $f$ 的估计。

Verification Flow

然而，对于大多数问题，一个固定的 $h$ 显然是不能得到很好的估计的，否则，岂不是大量问题有了通解？因此，我们真正需要的 learning 是从假设空间 $\mathcal{H}$ 中选取一个针对特定问题合适的 $h$ ，那么，选择的流程是怎样的？

• 
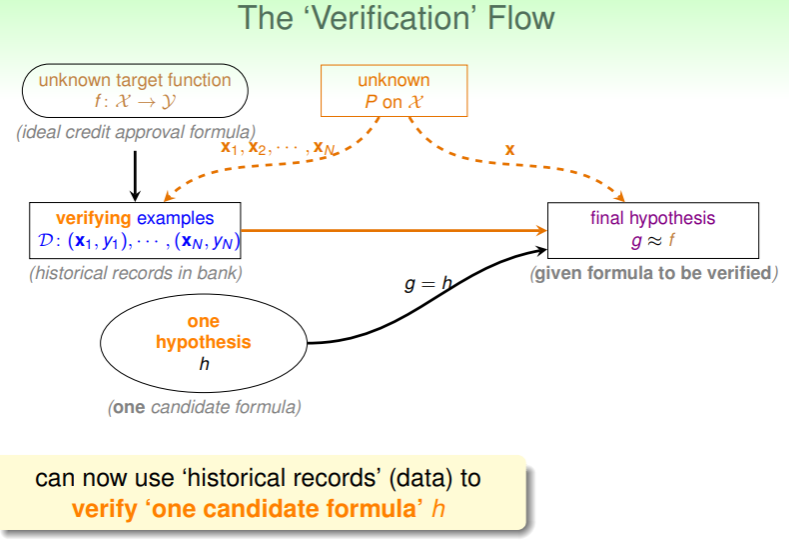
• 对于一个假设 $h$ ，我们需要找一些新的资料（即测试集，verify/test examples），看看从之前旧的数据中获得的 $h$ 是否还能在新的资料里足够优秀；

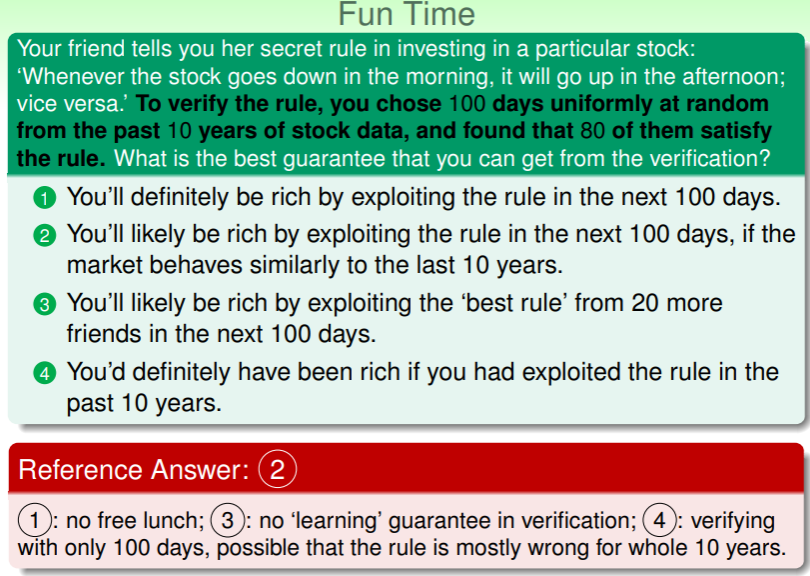
练习：由过去推导未来

Connection to Real Learning

BAD data

从概率推广到机器学习的理论还不够，我们很容易从前文得知，一切估计都基于预测的概率，那么必然会出现各种奇奇怪怪的情形：

• 我们从同一个罐子里抽样，每次获取的都是局部的信息，局部信息千差万别，可以尽信吗？当然不行，但，为何不行？什么又是行的呢？从概率论的角度，我们可以知道抽样的结果全为非橙色小球的概率极小 $(1-\mu {)}^N$，但只要取样次数 M 足够大，总还是有可能发生的：$1-((1-\mu {)}^N{)}^M\approx 1$ ：

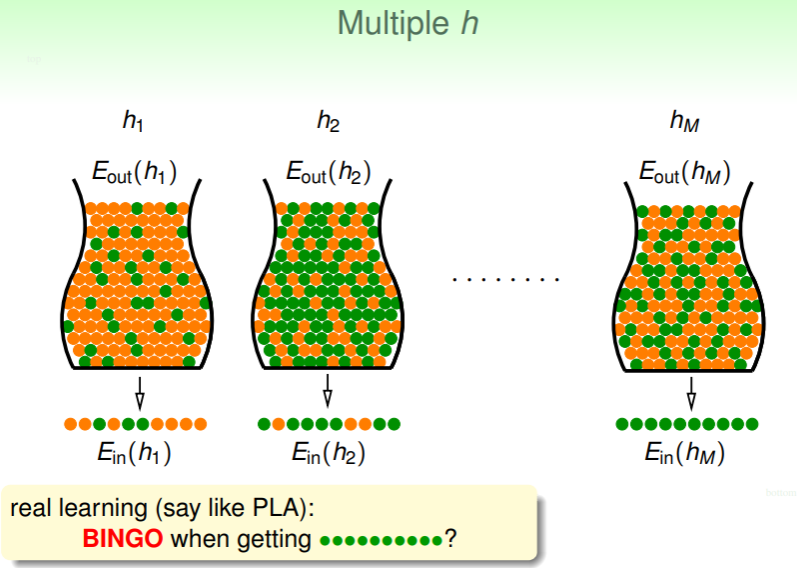
我们把 $E_{in}$ 和 $E_{out}$ 差距过大的采样，称为 BAD sample ，其会导致糟糕的预测结果。类似的，对于一个特定的假设 $h$ ，在某个抽样集 $\mathcal{D}$ 上产生的 $E_{in}$ 远小于全局的 $E_{out}$，就称其为 BAD data 。Hoeffding 不等式能够保证对于单个假设 $h_i$ ，其在不同采样的 ${\mathcal{D}}_i$ 上是 BAD data 的概率很小：

$$\text{Prob}[BAD\mathcal{D}]=\sum _{\text{all possible }\mathcal{D}}\text{Prob}(\mathcal{D})\cdot [BAD\mathcal{D}]$$

但如果对于 M 个假设 $h$ ，每个假设都或多或少在样本 ${\mathcal{D}}_i$ 上是 BAD data，如果只要样本 ${\mathcal{D}}_i$ 对某个 $h_i$ 是 BAD data，就标记为 BAD ，那有没有 ${\mathcal{D}}_j$ 对所有假设 $h$ 都不是 BAD 的呢？这样用它来进行训练得到准确度的概率必然更高：

• 
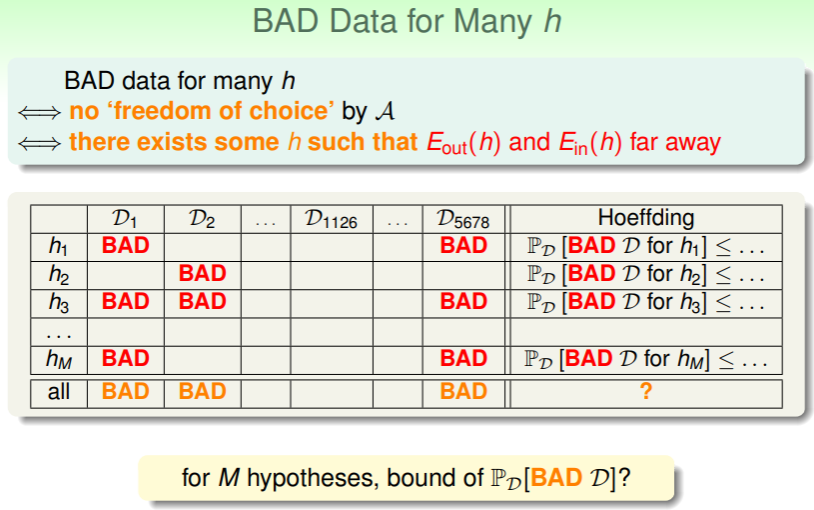
• 考查 ${\text{Prob}}_{\mathcal{D}}[BAD\mathcal{D}]$，可以使用概率加法公式求得上界：
• 这个式子告诉我们，不必知道 $E_{out}(h_m)$ 的确切数据，我们仍能在犯错概率不超过 $\frac{2M}{e^{2{ϵ}^{2}N}}$ 的情况下认为 $E_{in}(g)\approx E_{out}(g)$ 是 PAC 的，无论学习算法 $\mathcal{A}$ 是什么；

这也就佐证了前文我们直接选取 $E_{in}(h_m)$ 最小的假设 $h_m$ 作为 g 的可行性。

Statistical Learning Flow

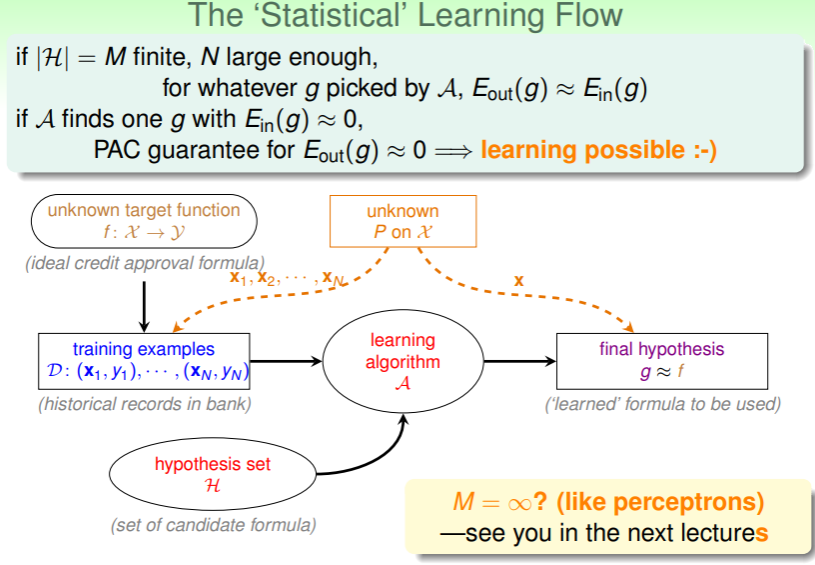
• 总之，对于有限大小的假设集 $\mathcal{H}$，只要采样数据 N 足够大，那么通过学习算法选出的估计 g，都能够满足 $E_{out}(g)\approx E_{in}(g)$ ，
• 如果能够找到 $E_{in}(g)\approx 0$，那么就能 PAC 地认为 $E_{out}\approx 0$ 也成立；

练习：理解 BAD data 与犯错概率的上界