20-Dual-Support-Vector-Machine

Motivation of Dual SVM

上节课提到，我们要实现非线性的 SVM ，就必须要借助特征转换这个工具：

$$\underset{b,\mathbf{w}}{\min }\frac{1}{2}{\mathbf{w}}^T\mathbf{w}\text{ s.t. }{y}_n({\mathbf{w}}^T\underset{\Phi ({\mathbf{x}}_n)}{\underbrace{{\mathbf{z}}_n}}+b)\ge 1,\text{ for }n=1,2,...,N$$

不过在涉及到特征转换时，要求解这个 QP 问题就会比较麻烦：

• 
• 这里 $\tilde{d}$ 就是特征转换的空间维数，QP 的解法就与 $\tilde{d}+1$ 个变量和样本规模 $N$ 的限制有关，当 $\tilde{d}$ 非常大时，计算效率很低；

因此我们的目标是移除 SVM 在空间维数 $\tilde{d}$ 上的依赖：

• 我们提出等价的 SVM ，称为 Dual SVM（对偶支持向量机），其只与样本规模 N 有关：

Regularization and Dual SVM

那么如何实现这种等价互换呢？回想之前使用 正则化 对高维空间的限制：

• 
• 在这里，左右两式可以通过求梯度 $\nabla E_{in}(\mathbf{w})+\frac{2\lambda }{N}\mathbf{w}=0$ 建立联系，从而得知 $C$ 与 $\lambda (\ge 0)$ 实际上是等价的，在正则化中我们将 $\lambda$ 视作 $C$ 的一个替代；

那么在 Dual SVM 中，我们也将 $\lambda$ 视作未知的既定限制，作为变量来求解，并且 SVM 中限制条件数与输入样本的规模相同（限制条件为 $E_{in}=0$ ，即对所有输入样本的判断都正确），因此作为变量求出的 $\lambda$ 数量将会有 $N$ 个。故，原本有条件限制的 SVM 问题：

$$\underset{b,\mathbf{w}}{\min }\frac{1}{2}{\mathbf{w}}^T\mathbf{w}\text{ s.t. }{y}_n({\mathbf{w}}^T{\mathbf{z}}_n+b)\ge 1,\text{ for }n=1,2,...,N$$

就可以利用拉格朗日乘子 ${\lambda }_n{\alpha }_n$ 设立拉格朗日函数，求解极值：

$$\mathcal{L}(b,\mathbf{w},\alpha )=\underset{\text{objective}}{\underbrace{\frac{1}{2}{\mathbf{w}}^T\mathbf{w}}}+\sum _{n=1}^N{\alpha }_n(\underset{\text{constraint}}{\underbrace{1-y_n({\mathbf{w}}^T{\mathbf{z}}_n+b)}})$$

这里 objective 部分就是要求解的极小值的部分，constaint 部分就是限制条件 ${\lambda }_n$ （这里与大陆课本的拉格朗日函数不同，${\alpha }_n$ 实际上充作了课本中的那个作为限制条件的系数的 $\lambda$ ，这里的差异不过是为了前后 $\lambda$ 符号的含义统一，无需疑虑）

现在，我们可以将 SVM 问题看作是求解拉格朗日函数的问题：

$$SVM\equiv \underset{b,\mathbf{w}}{\min }\left(\underset{\text{all }{\alpha }_n\ge 0}{\max }\mathcal{L}(b,\mathbf{w},\alpha )\right)$$

这里要分析，

• 如果拉格朗日函数中限制条件 $1-y_n({\mathbf{w}}^T{\mathbf{z}}_n+b)$ 为正，说明这样的 $\mathbf{w}$ 违反了限制，要使得拉格朗日函数最大，就会一直增长到无穷大；
• 而若限制条件为负，则说明可行，因此拉格朗日函数最大也不超过 $\frac{1}{2}{\mathbf{w}}^T\mathbf{w}$ ；

最终，我们将 SVM 中的限制纳入了对拉格朗日函数求最值的问题中。

练习：写出拉格朗日函数的形式

Lagrange Dual SVM

我们继续思考上述的拉格朗日函数，由于其要取 $\max$ ，因此在 ${\alpha }_n^{{}^{\prime }}>0$ 前提下，任意特定 ${\alpha }^{{}^{\prime }}$ 都满足：

$$\underset{b,\mathbf{w}}{\min }\left(\underset{\text{all }{\alpha }_n\ge 0}{\max }\mathcal{L}(b,\mathbf{w},\alpha )\right)\ge \underset{b,\mathbf{w}}{\min }\mathcal{L}(b,\mathbf{w},{\alpha }^{{}^{\prime }})$$

因此，选择所有 ${\alpha }_n^{{}^{\prime }}$ 中最佳的 ${\alpha }^{{}^{\prime }}$ ，也可以满足上面的关系，即：

$$\underset{b,\mathbf{w}}{\min }\left(\underset{\text{all }{\alpha }_n\ge 0}{\max }\mathcal{L}(b,\mathbf{w},\alpha )\right)\ge \underset{\text{Lagrange dual problem}}{\underbrace{\underset{\text{all }{\alpha }_n^{{}^{\prime }}\ge 0}{\max }\underset{b,\mathbf{w}}{\min }\mathcal{L}(b,\mathbf{w},{\alpha }^{{}^{\prime }})}}$$

右侧式子称为该拉格朗日问题的对偶问题。不过此时左右两式关系是 $\ge$ ，称为 weak duality ；如果能够证明为 $=$ 关系，那就可以解右式从而得到左式的解，这称为 strong duality 。经过 QP 问题的研究，如果目标问题满足：函数为凸、原问题有解、线性条件限制，那么 $=$ 就成立，幸运的是，在这里刚好满足这三个条件（constraint qualification）。

Solution for Langrange Dual Problem

因此，我们可以展开右侧对偶式进行求解：

$$\underset{\text{all }{\alpha }_n\ge 0}{\max }\left(\underset{b,\mathbf{w}}{\min }\underset{\mathcal{L}(b,\mathbf{w},\alpha )}{\underbrace{\frac{1}{2}{\mathbf{w}}^T\mathbf{w}+\sum _{n=1}^N{\alpha }_n(1-y_n({\mathbf{w}}^T{\mathbf{z}}_n+b))}}\right)$$

该式内部的拉格朗日函数的最小值即是在“谷底”，我们可以通过求解梯度来获得：

$$\begin{array}{r}\frac{\partial \mathcal{L}(b,\mathbf{w},a)}{\partial b}=0=-\sum _{n=1}^N{\alpha }_n{y}_n=0\end{array}$$

既然最佳解最后必然满足这个条件，那么我们在求解最小值前就先将这个条件附加上，那么就可以得到：

$$\underset{\text{all }{\alpha }_n\ge 0,\sum _{n=1}^N{\alpha }_n{y}_n=0}{\max }\left(\underset{b,\mathbf{w}}{\min }\frac{1}{2}{\mathbf{w}}^T\mathbf{w}+\sum _{n=1}^N{\alpha }_n(1-y_n({\mathbf{w}}^T{\mathbf{z}}_n))\right)$$

，另一方面，在“谷底”对 $\mathbf{w}$ 也会满足：

$$\begin{array}{r}\frac{\partial \mathcal{L}(b,\mathbf{w},a)}{\partial w_i}=0=w_i-\sum _{n=1}^N{\alpha }_n{y}_n{z}_{n,i}\end{array}$$

写成向量形式，就是：

$$\mathbf{w}=\sum _{n=1}^N{\alpha }_n{y}_n{\mathbf{z}}_n$$

同理，我们可以最终化简问题为：

$$\begin{array}{r}\underset{\text{all }{\alpha }_n\ge 0,\sum _{n=1}^N{\alpha }_n{y}_n=0,\mathbf{w}=\sum _{n=1}^N{\alpha }_n{y}_n{\mathbf{z}}_n}{\max }\left(\underset{b,\mathbf{w}}{\min }\frac{1}{2}{\mathbf{w}}^T\mathbf{w}+\sum _{n=1}^N{\alpha }_n-{\mathbf{w}}^T\mathbf{w}\right)\\ ⟺\underset{\text{all }{\alpha }_n\ge 0,\sum _{n=1}^N{\alpha }_n{y}_n=0,\mathbf{w}=\sum _{n=1}^N{\alpha }_n{y}_n{\mathbf{z}}_n}{\max }-\frac{1}{2}||\sum _{n=1}^N{\alpha }_n{y}_n{\mathbf{z}}_n|{|}^2+\sum _{n=1}^N{\alpha }_n\end{array}$$

因此，这最后就变成只有 ${\alpha }_n$ 的一个最大化问题。

上述的过程中用到的限制条件称为 KKT Optimality Conditions ：

• 
• 这些条件是：原问题可解、可以实现对偶、对偶后的内部可以求得最优解、原问题的内部也可以求得最优解；
• 从此，找到最优的 $\alpha$ 就可以求解原问题。

练习：理解 KKT 条件

Solving Dual SVM

Specific QP Solver is Better

将上文最终的对偶问题写成最小化的形式，我们就可以得到：

$$\begin{array}{rl}& \underset{\alpha }{\min }\frac{1}{2}\sum _{n=1}^N\sum _{m-1}^N{\alpha }_n{\alpha }_m{y}_n{y}_m{\mathbf{z}}_n^T{\mathbf{z}}_m-\sum _{n=1}^N{\alpha }_n\\ & \text{ subject to }\sum _{n=1}^N{y}_n{\alpha }_n=0;{\alpha }_n\ge 0,\text{ for }n=1,2,...,N;\end{array}$$

即，我们实现了本堂课开头的转换——将 SVM 问题转换为 $N$ 个变量、$N+1$ 个限制的对偶问题。那么如何解这个问题呢？当然还是 QP 问题：

• 
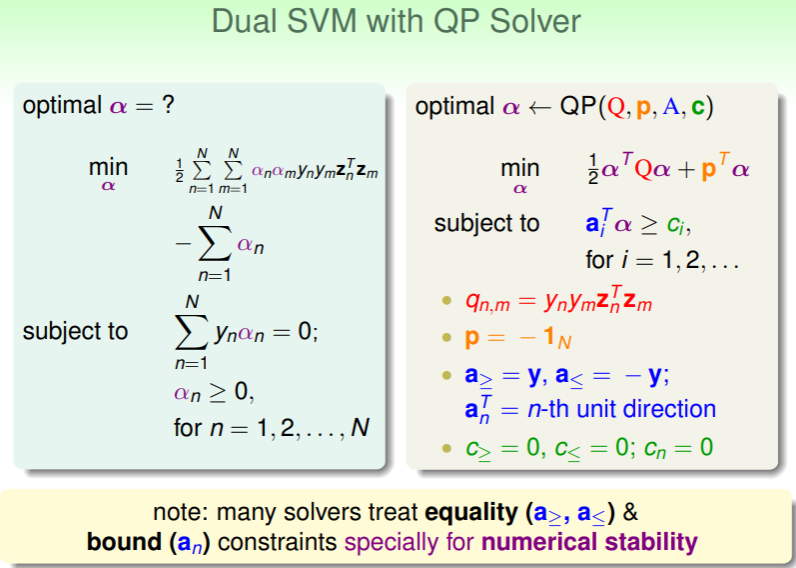
• 不过这个 QP 问题直接套用这种通用的 QP solver 的话，还需要进行一些考量：
  • 在该对偶问题中当样本数 $N$ 极大时，仅用于存放 $Q_D$ 这个稠密矩阵都将会占用过多的内存空间，因此有特定的针对 SVM 问题的 QP solver ，可以不必存储它；

回过头来从 KKT 条件中审视这个找最优的问题，我们可以得知：

• 
• 要求得最佳的 $\mathbf{w}$ ，就要求得最佳的 $\alpha$ ，
• 而要求得最佳的 $b$ ，则在 ${\alpha }_n>0$ 条件下，可以推得 $b=y_n-{\mathbf{w}}^T{\mathbf{z}}_n$ 这样一系列的解，$b$ 代表着 SVM 可以活动的范围——就是 SVM boundary 的宽度；

练习：算出最佳的 b

Message behind Dual SVM

SV Candidate ?

还记得之前我们说 SVM 边界上的点其实是 候选者 （candidate）吗？现在从 Dual SVM 的角度，我们再来审视这个候选者的说法：

• 
• 在 Dual SVM 中，我们会对样本添加一个 ${\alpha }_n$ ，只有边界上点的 $\alpha >0$ ，才有考虑的价值，此时它才从候选者中脱颖而出——成为真正的 Support Vector ；
• 因此，只有真正的支撑向量在计算 $\mathbf{w}$ 和 $b$ 时才会贡献价值：
  • 计算 $\mathbf{w}$ 时要考虑所有 SV ：$\mathbf{w}=\sum _{n=1}^N{\alpha }_n{y}_n{\mathbf{z}}_n=\sum _{SV}{\alpha }_n{y}_n{\mathbf{z}}_n$ ，
  • 计算 $b$ 时只需要一个 SV 即可：$b=y_n-{\mathbf{w}}^T{\mathbf{z}}_n,\text{with any SV}({\mathbf{z}}_n,y_n)$；

SVM and PLA

通过对偶问题，我们可以求解得 ${\alpha }_n$ ，从而求出 SVM 的最佳权重向量 ${\mathbf{w}}_{SVM}=\sum _{n=1}^N{\alpha }_n{y}_n{\mathbf{z}}_n$ ，这个式子似乎有些熟悉？回顾 PLA 中的权重向量求解公式：

• 
• 我们可以得知，这两种模型的 $\mathbf{w}$ 都是原始资料的线性组合，并且这个结论对从 ${\mathbf{w}}_0=0$ 开始做对梯度下降或随机梯度下降的逻辑回归或线性回归也是成立的，这时 $\mathbf{w}$ 就称为由原始资料能够表示的最佳权重；
• 因此所谓 SVM ，就是可以仅有 SV 表示最佳权重 $\mathbf{w}$ 的模型；

Primal SVM Vs. Dual SVM

上节课我们讲述的 Primal SVM 和这节课讲的 Dual SVM 究竟有什么区别与联系呢？

• Primal SVM 适合在样本维数 $\tilde{d}$ 较小时使用，它的物理含义就是通过特殊的放缩找到最佳的 $(b,\mathbf{w})$ ；
• Dual SVM 通过对偶问题，规约了样本维数，使 SVM 直接关联样本数，它的物理含义就是找到真正的 SV 和对应的 ${\alpha }_n$ ，通过这些重建 SVM 边界；
• 二者最后都会得到最佳的 $(b,\mathbf{w})$ ，从而找到最合适的 hyperplane ，最终求得 $g_{SVM}=(\mathbf{x})=\text{sign}({\mathbf{w}}^T\Phi (\mathbf{x})+b)$ ；
• 

Hidden Dimension

还记得这节课的目标吗？我们想要消除样本维数 $\tilde{d}$ 对 SVM 求解时的性能限制，Dual SVM 确实解决了一部分，但它真的消除了对 $\tilde{d}$ 的依赖了吗？其实在计算 QP 问题的 $Q_D=y_n{y}_m{\mathbf{z}}_n^T{\mathbf{z}}_m$ 矩阵里，这个内积的计算仍然是在 ${\mathbb{R}}^{\tilde{d}}$ 空间中的，因此还是对其有依赖的。

下节课我们将进一步避开在 ${\mathbb{R}}^{\tilde{d}}$ 中的计算，且听下回分解。

练习：计算 SV candidates