区间问题
905. 区间选点
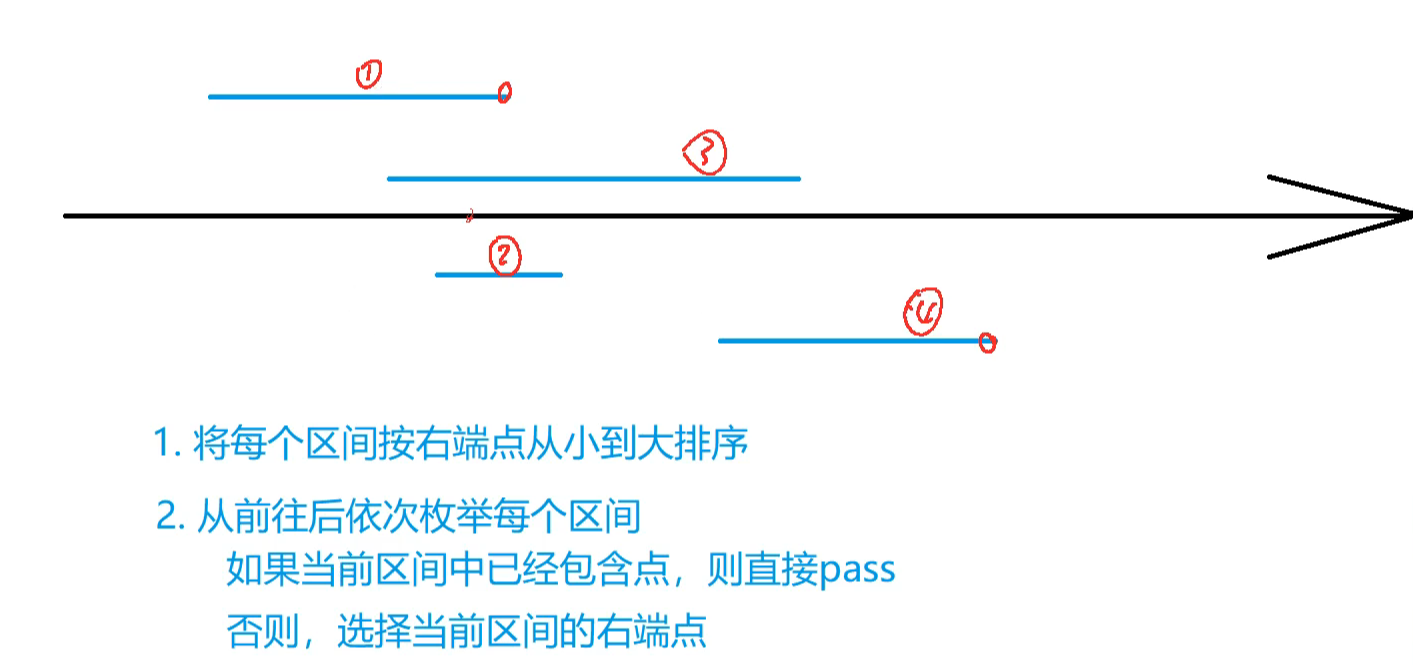
// 区间选点
#include <algorithm>
#include <iostream>
using namespace std;
typedef pair<int, int> PII;
const int N = 100010;
PII interval[N]; // 存放区间的数组,pair.first存放闭区间的左端,second存放闭区间的右端
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> interval[i].first >> interval[i].second;
}
// 使用lambda表达式按照区间的右端点从小到大排序
sort(interval, interval + n, [](const PII &a, const PII &b) {
return a.second < b.second;
});
// 贪心策略,从前往后逐个枚举每个区间的右端点,如果当前区间包含该点,就pass并查询下一个区间,
// 否则包含当前区间的右端点
int count = 0; // 选取的点的数量
int endPoint = -1e9 - 10; // 上一个选取的点的位置,初始化为一个非常小的数
for (int i = 0; i < n; i++) {
// 如果当前区间的左端点大于上一个选取的点的位置,则需要在当前区间选取一个新的点
if (interval[i].first > endPoint) {
count++; // 增加选点的数量
endPoint = interval[i].second; // 更新上一个选取的点的位置为当前区间的右端点
}
}
cout << count << endl;
return 0;
}908. 最大不相交区间数量
// 最大不相交区间的数量
#include <algorithm>
#include <iostream>
using namespace std;
const int N = 100010, INF = 1e9 + 10;
struct Range {
int l, r; // 区间左右端点
bool operator<(const Range &W) const { // 重载运算符
return r < W.r;
}
} range[N]; // 存放区间的结构体数组
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> range[i].l >> range[i].r;
}
// 使用重载后的运算符,按照区间的右端点从小到大排序
sort(range, range + n);
// 贪心策略,从前往后逐个枚举每个区间的右端点,如果当前区间的左端点小于等于上一个区间的右端点,就pass并查询下一个区间,
// 否则包含当前区间的右端点
int count = 1; // 选取的不想交区间的数量
int endPoint = range[0].r; // 上一个选取的点的位置,初始化为第一个区间的右端点
for (int i = 1; i < n; i++) {
// 如果当前区间的左端点小于等于上一个区间的右端点,跳过,否则计数+1
if (range[i].l > endPoint) {
count++; // 更新不相交区间的计数
endPoint = range[i].r; // 更新上一个选取的点的位置为当前区间的右端点
}
}
cout << count << endl;
return 0;
}906. 区间分组
// 区间分组
#include <algorithm>
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
typedef pair<int, int> PII;
vector<PII> intervals;
bool cmp(const PII &a, const PII &b) { return a.first < b.first; }
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
int l, r;
cin >> l >> r;
intervals.push_back({l, r});
}
// 使用自定义的比较函数,按照区间的左端点从小到大排序
sort(intervals.begin(), intervals.end(), cmp);
// 贪心策略,按每个区间的右端点从小到大逐个枚举,堆里存已检查分组的最小右端点,
// 当前要判断的区间的左端点至少要大于已检查分组中的某个右端点,才不用开新组,
// 若小于 / 等于所有分组的最小右端点(也就是小于 / 等于堆顶),则需要开新组
priority_queue<int, vector<int>, greater<int>> heap; // 优先队列,存储每个组的最大右端点
for (const auto &r : intervals) {
if (!heap.empty() && heap.top() < r.first) {
// 如果当前区间的左端点大于堆顶元素(也就是目前所有组中最小的右端点),
// 则可以复用这个组
heap.pop(); // 移除这个组的旧的右端点
}
// 将当前区间的右端点加入优先队列(代表开启新组或加入现有组)
heap.push(r.second);
}
cout << heap.size() << endl;
return 0;
}为什么这里要用左端点排序呢?
按左端点排序
- 贪心策略的正确性:当我们按照左端点从小到大对区间进行排序时,我们实际上是在按照区间的开始顺序来组织这些区间。这样做的好处是,对于任何一个给定的区间,如果它不能加入到当前的任何一个组中(即它的左端点小于或等于当前组的最大右端点),那么它必须开启一个新的组。因为之后的所有区间的左端点都将更大,所以它们也不可能加入到当前的组中。
- 最小化分组数:这种排序方式有助于最小化所需的分组数。因为我们总是尝试将当前的区间加入到已有的组中(如果可能的话),并且这种尝试是基于区间开始顺序进行的,这有助于我们尽可能地利用每个组,从而减少总的分组数。
- 简化逻辑:按照左端点排序还简化了实现逻辑。我们只需依次考虑每个区间是否能加入到某个现有组中(基于右端点)。如果不能,则开启新组。这种逻辑非常直接,易于实现。
按右端点排序 按照右端点排序虽然也是一种常见的排序策略,但在区间分组问题中,它并不适用。这是因为:
- 当区间按照右端点排序时,我们确实可以确保每个选择的点都能覆盖尽可能多的区间(例如,在区间选点问题中)。但在区间分组问题中,我们的目标是最小化分组数量,而不仅仅是覆盖所有区间。按照右端点排序,不能保证尽可能多地利用每个组,因为一个区间的结束不一定告诉我们它是否能与之前的区间形成不相交的组。
907. 区间覆盖

// 区间覆盖
#include <algorithm>
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
typedef pair<int, int> PII;
vector<PII> intervals;
int main() {
int s, t; // 指定要覆盖的区间[s,t]
cin >> s >> t;
int n;
cin >> n;
for (int i = 0; i < n; i++) {
int l, r;
cin >> l >> r;
if (r >= s && l <= t) // 只有当区间与[s,t]有交集时才需要考虑
intervals.push_back({l, r});
}
if (intervals.empty()) { // 如果没有能够覆盖的区间,自然输出-1结束即可
cout << -1 << endl;
return 0;
}
sort(intervals.begin(), intervals.end()); // pair的排序是按照first元素进行,本题也需要按左端点排序
// 从前向后依次枚举每个区间,在所有能够覆盖s的区间中,选择右端点最大的区间,然后将s更新成该最大右端点的值
int ans = 0; // 记录所需的最少区间数量
bool can_cover = false; // 记录是否能完全覆盖[s,t]
for (int i = 0, maxR = -1e9 - 10; s <= t && i < intervals.size();) {
can_cover = false;
// 寻找能覆盖当前起点s,并且右端点最远的区间
for (; i < intervals.size() && intervals[i].first <= s; ++i) {
if (intervals[i].second > maxR) {
maxR = intervals[i].second;
can_cover = true;
}
}
if (can_cover) { // 如果找到了能覆盖当前起点的区间
++ans; // 区间数量+1
s = maxR; // 更新当前的起点为找到的区间的右端点
} else {
break; // 如果没有找到能覆盖当前起点的区间,说明无法覆盖整个[s,t],退出循环
}
}
if (s < t) { // 检查是否完全覆盖了[s,t]
cout << -1 << endl; // 不能完全覆盖时输出-1
} else {
cout << ans << endl; // 能完全覆盖时输出最少区间数量
}
return 0;
}Huffman 树
148. 合并果子
// 合并果子
#include <iostream>
#include <queue>
using namespace std;
const int N = 100010;
priority_queue<int, vector<int>, greater<int>> heap;
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
int a;
cin >> a;
heap.push(a);
}
int res = 0;
while (heap.size() > 1) {
int a = heap.top();
heap.pop();
int b = heap.top();
heap.pop();
res += a + b;
heap.push(a + b);
}
cout << res;
return 0;
}排序不等式
913. 排队打水
#include <algorithm>
#include <iostream>
#include <queue>
using namespace std;
int main() {
int n;
scanf("%d", &n);
priority_queue<int, vector<int>, greater<int>> heap;
while (n--) {
int x;
scanf("%d", &x);
heap.push(x);
}
long long res = 0;
while (heap.size() > 1) {
int a = heap.top();
heap.pop();
res += a * heap.size();
}
cout << res << endl;
return 0;
}绝对值不等式
104. 货仓选址
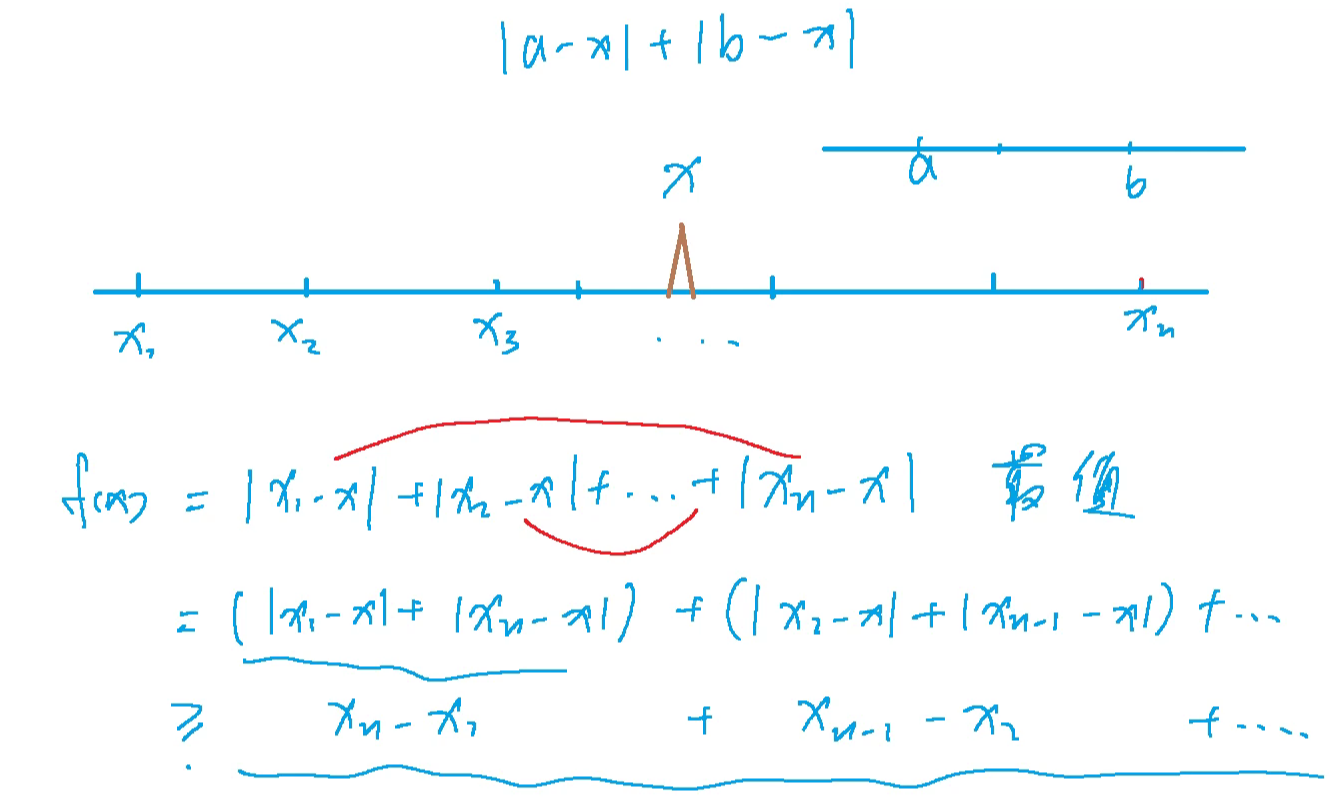
// 货仓选址
#include <algorithm>
#include <iostream>
using namespace std;
const int N = 100010;
int n;
int q[N];
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d", &q[i]);
sort(q, q + n);
int res = 0;
for (int i = 0; i < n; i++) res += abs(q[i] - q[n / 2]);
printf("%d\n", res);
return 0;
}推公式
125. 耍杂技的牛

// 耍杂技的🐮
#include <algorithm>
#include <iostream>
using namespace std;
typedef pair<int, int> PII;
const int N = 50010;
int n;
PII cow[N];
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) {
int s, w;
scanf("%d%d", &w, &s);
cow[i] = {w + s, w};
}
sort(cow, cow + n);
int res = -2e9, sum = 0;
for (int i = 0; i < n; i++) {
int s = cow[i].first - cow[i].second, w = cow[i].second;
res = max(res, sum - s);
sum += w;
}
printf("%d\n", res);
return 0;
}压力最大的牛一定是最底层的牛,我们的算法让 w+s 最大的放在最下面,可以分成两种情况去看:
- w 很大,s 很小:由于 w 最大的牛在最下面,对其余牛造成的压力自然较小,可能能达到最小的最大压力
- w 很小,s 很大:这种情况是完美的情况,最强壮的牛放在最下面,可能能达到最小的最大压力
因此我们按照 w+s 从小到大去排列。