2012_13-final

这两年的是回忆版，仅收集一些有价值的题目。

判断

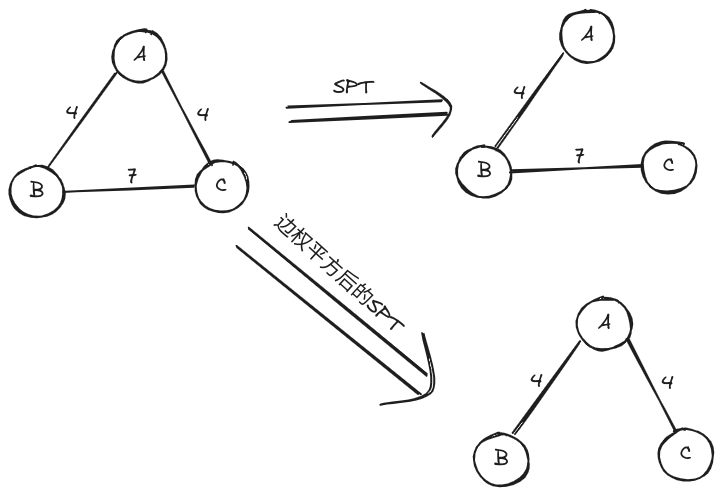
1. 对于正权值的有向图，如果把所有的边权都平方处理，则用 Dijkstra 算法得到的 SPT 形态不变。

❌

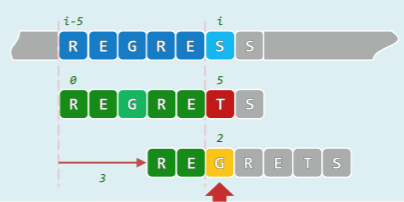
2. KMP 匹配过程中，当主程序运行到 i、j 的状态时，意味着之前至少做过 i 次成功匹配及 i-j 次失败匹配。

❌

3. 如果使用线性复杂度的中位数选取算法，快速排序的复杂度可以保证在最坏情况下也渐进等于 $O(n\log n)$

✅

选择

1. 将 [1481,1992) 区间内的整数逐一插入到空 AVL 树中，最后得到该树的高度为（ E B ） A. 7 B. 8 C. 9 D. 10 E. 以上都错

Fib-AVL 树的形态，因此其高度与节点数的关系是 $fib(h+3)-1\le n$ ，此处 n=512，而 fib (15)-1 = 609, fib (14)-1 = 376，因此高度 h=14-3=11

❌ 上面做错了，这并不是一个 Fib-AVL 树。 习题解析 7-20：证明递增插入2^(h+1)-1个关键码到AVL树必能得到满树

本题中关键码数=1992-1481=511= $2^{8+1}-1$ ，因此树高为 8.

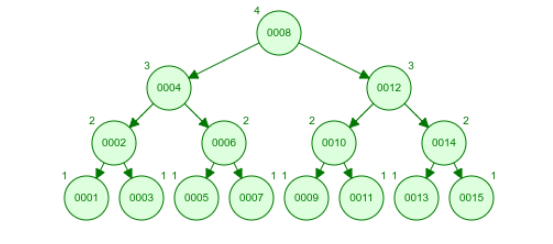
2. 将 [23,1481) 区间内的整数组成一棵 2-3 BTree，且根节点只有一个关键码，则最终该 BTree 的高度至少是（ E ） A. 7 B. 8 C. 9 D. 10 E. 以上都错

BTree 的根节点关键码只有一个，则考虑其左右子树，不妨设左子树的关键码数为 729、右子树的关键码规模为 728，因此左子树的高度最低为 $\lceil {\log }_{3}729+1\rceil =7$，因此加上根节点，整个 BTree 的高度为 8。

至于右子树，由于 BTree 是左右平衡的，左子树因为超过了临界点而达到 7层，因此右子树虽不超过临界点，但应当是松散地达到 7 层。

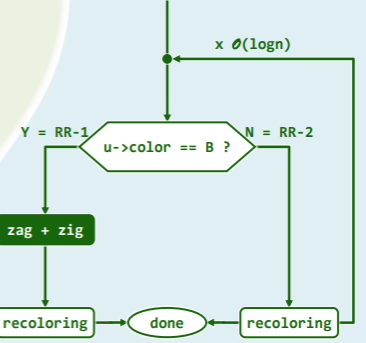
3. 对红黑树进行插入操作时，若发生双红修正，且黑高度增加，则（ A ）发生重染色，（ B ）发生结构调整。 A. 必然 B. 可能 C. 必然不

红黑树双红修正：黑高度增加的可能性

4. 针对以下各搜索树进行删除操作，哪些树可能会经过 $\Omega (\log n)$ 次局部调整，其中 n 为关键码的数量。（ A, B, D ） A. AVL B. Splay C. Red-black D. BTree E. 都不会

Fib-AVL 删除中序遍历最小的节点。 Splay 树删除前的查找就会通过 $\Omega (\log n)$ 次旋转上升至根。 Red-black 树本身的特性就是插入或删除对整体形态的变化影响为 $O(1)$，更准确地： BTree 在递增序列插入结束后，当根节点的关键码为 1 时，删除之，则会引发 $O(\log n)$ 次局部调整。

5. 左式堆中，左子堆一定大于右子堆的参数是（ A ） A. NPL B. 规模 C. 高度 D. 外部节点数

解答

KMP

构造如下两个模式串的 next[] 和改进版 next[]：

     j:        0   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15
   P[j]:       S   H   I   P   S   H   I   P   E   D   _   S   H   I   P   S
  next[j]:    -1   0   0   0   0   1   2   3   4   0   0   0   1   2   3   4
imp-next[j]:  -1   0   0   0  -1   0   0   0   4   0   0  -1   0   0   0  -1

就地堆排序

Heapsort 过程

对以下整型向量做就地堆排序，试给出（采用R. Floyd 算法）建堆以及此后各步迭代中向量的内容。

A[0,15):    50  63  8  25  54A  45  36  91  83A  88  83B  15  54B  58  13
heapify():
            ......................  58  .........................  36  13
		    ..................  54B 58  ................. 15  45   36  13
			............... 88  54B 58  ........ 54A 83B  15  45   36  13
			.......... 91   88  54B 58  25  83A  54A 83B  15  45   36  13
递归地下滤  ........58 91   88  54B 36  25  83A  54A 83B  15  45    8  13
			....91  58 83A  88  54B 36  25  63   54A 83B  15  45    8  13
			91  88  58 83A  83B 54B 36  25  63   54A  50  15  45    8  13

rank():
			0
			    1   2
					    3    4   5   6
									     7   8    9   10   11  12   13  14

heapsort():
			88  83A ..  63  ............... 13 ........................ 91
			83A 83B ..  63  54A ........... 13    8 ............... 88  91
			83B 63  ..  45  54A ........... 13    8 .......... 83A  88  91
			63  54A ..  45   50 ....... 25  13    8   15  83B  83A  88  91
			58  54A 54B 45   50  15 36  25  13    8   63  83B  83A  88  91
			54A 50  54B 45    8  15 36  25  13   58   63  83B  83A  88  91
			54B 50  36  45    8  15 13  25  54A  58   63  83B  83A  88  91
			50  45  36  25    8  15 13 54B  54A  58   63  83B  83A  88  91
			45  25  36  13    8  15 50 54B  54A  58   63  83B  83A  88  91
			36  25  15  13    8  45 50 54B  54A  58   63  83B  83A  88  91
			25  13  15   8   36  45 50 54B  54A  58   63  83B  83A  88  91
			15  13   8  25   36  45 50 54B  54A  58   63  83B  83A  88  91
			13   8  15  25   36  45 50 54B  54A  58   63  83B  83A  88  91
			8   13  15  25   36  45 50 54B  54A  58   63  83B  83A  88  91

指向原始笔记的链接

散列

给定 M=17 的散列表，Hash 函数为除余法、冲突解决方案为单向平方试探、删除策略为懒惰删除，对给定的一系列操作，给出每次操作后的散列表的状态。

只有光秃秃一个题干，不过没什么难度。