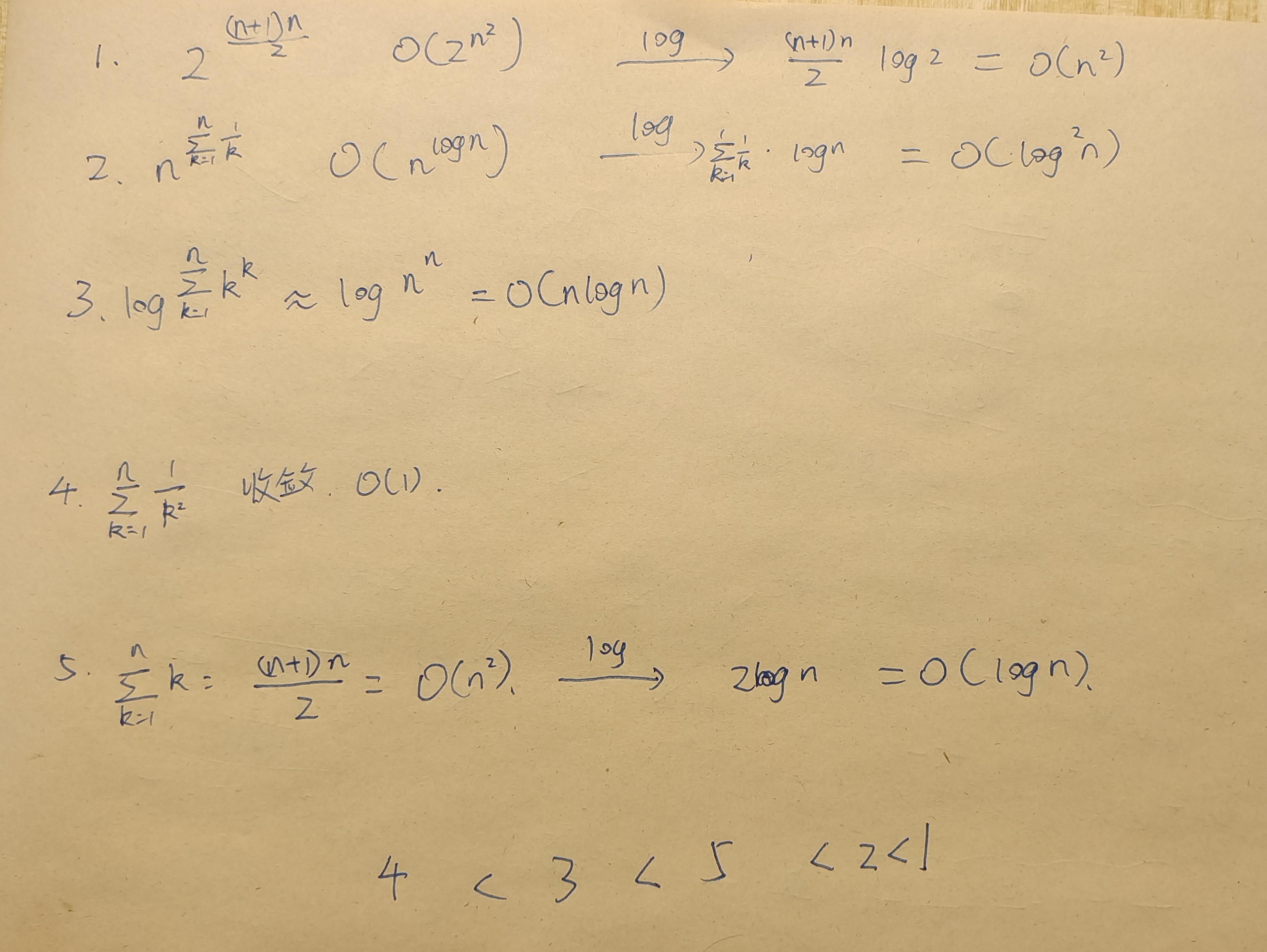2019-mid

判断

1. 使用容量为1009的辅助队列，足以对任一由2019个节点构成的二叉树做层次遍历。

❌ 习题 5-28：层次遍历辅助队列容量问题

• 只要辅助队列 Q 的容量不小于 $\lceil \frac{n}{2}\rceil$，就不致于中途出现溢出问题，但此题中 $\lceil \frac{2019}{2}\rceil =1010$，故会溢出。

2. 由 2019 个无差别节点构成的真二叉树，与由 1009 对括号构成的合法表达式一样多。

✅ 2019 个节点的真二叉树中，叶子节点有 1010 个，内部节点 1009 个，因此其互异的形态数为 Catalan (1009)； 而 1009对括号构成的合法表达式有 Catalan (1009)种，故正确。

3. 无论是在 Turing Machine 模型还是 RAM 模型中，整数加法都属于基本运算，时间成本均可视作常数。

✅ 这两个模型是用来统计运行时间复杂度的，其中基本运算都是常数级，避免干扰整体的复杂度估算。

4. 插入/选择排序后，逆序对不致增多；

✅

5. 插入/选择排序后，循环节不致减少；

❌

• 习题 3-14：循环节：选择排序中无需交换的元素的数量
• 但是对插入排序，循环节数目与选择排序并不相似，而是恰好相反

6. 同一棵二叉树的前序、中序、后序遍历序列中，叶子节点的相对次序必然完全一致。

✅ 对于叶节点，其左子树和右子树均为空，因此前、中、后序的遍历都不会继续递归下去，而是访问自身，而无论前中后哪种遍历，都是从二叉树最左下角的叶节点向右开始延伸、遍历。

7. 调用栈中多帧可能对应同一函数的调用，且不一定紧密相邻；

[! note] ✅ 互相调用：

int f(x) { g(x--);}
int g(x) { f(x--);}

8. 最优 PFC 树交换深度不同的节点及其子树后，必然不是最优 PFC 树；

✅ 正确答案：❌

• 不考虑权重时，真完全树是最优 PFC 树；
• 但考虑权重时，交换深度不同的节点及其子树，有可能保持总代价不变；

选择

1. 插入排序算法的（ A, B, D ）特点，是选择排序算法所不具备的。 A. 输入敏感性 B. 支持在线计算 C. 就地性 D. 最好情况下复杂度更低

选择排序对输入不敏感、不支持在线计算、最好情况也需要 $O(n^2)$ 的时间复杂度。

2. 共有（ B ）种栈混洗方案，可使序列 <M,A,M,A,M,I,A]=A 转换为 B=[M,A,M,A,M,I,A> 。 A. 6 B. 7 C. 8 D. 9

对 A 中序列从栈顶到栈底做标记，依次为 1、2、3、4、5、6、7，则考查辅助栈的出栈序列，有以下几种满足要求的序列： 1234567 1254367 1432567 3214567 3254167 3452167 5432167

3. 函数调用栈按出栈顺序排列，恰好与二叉树的（ C ）遍历序列相同。 A. 先序 B. 中序 C. 后序 D. 层次

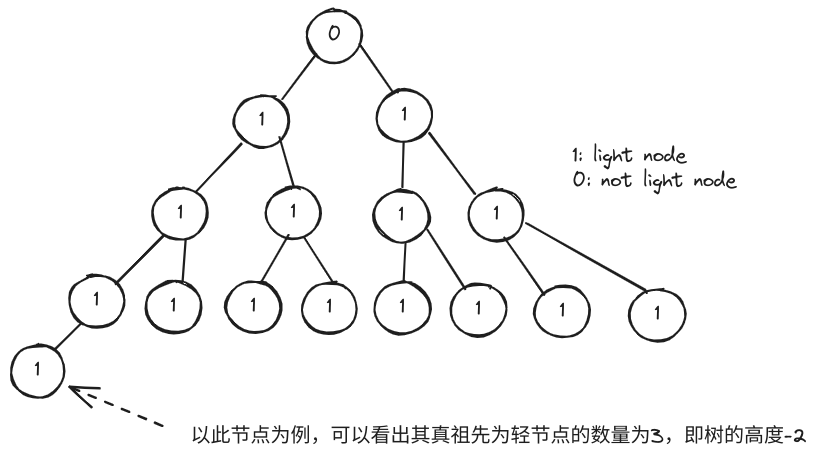
4. 如果将二叉树中满足 x.size <= x.parent.size/2 的非根节点 x 称作“轻节点”，那么在包含2019个节点的二叉树中，一个节点至多可能有（ C ）个轻的真祖先。 A. 9 B. 11 C. 8 D. 10

这个题比较复杂，轻节点与否是会动态变化的。 $\lceil {\log }_2(2019+1)\rceil -1-1=9$

解答

RPN

试将常规表达式 (0!+1)*2^(3!+4)+5!/6*(7-8)-9 转化为逆波兰表达式：

0! 1 + 2 3! 4 + ^ * 5! 6 / 7 8 - * + 9 -

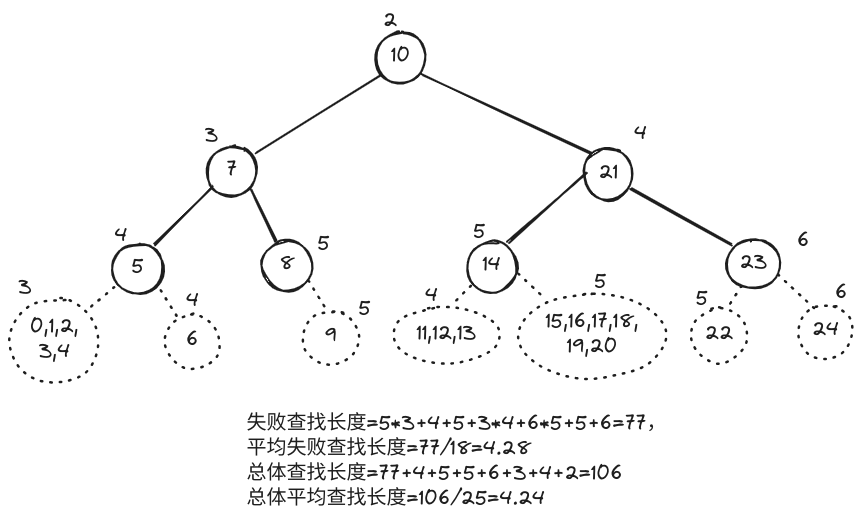
平均查找长度

设整数 e 随机取自 [0,25)，调用 binSearchA(_elem,e,0,7) 对如下整型有序向量做查找：

k:     0    1    2    3    4    5    6
A[k]:  5    7    8   10   14   21   23

则失败情况下的平均查找长度、总体的平均查找长度各是多少？请简要列出推算依据。

复杂度排序

$\prod _{k=1}^n{2}^k$, $n^{\sum _{k=1}^n\frac{1}{k}}$, $\log (\sum _{k=1}^n{k}^k)$, $\sum _{k=1}^n\frac{1}{k^2}$, $\sum _{k=1}^{n}k$ 1 2 3 4 5

试以渐进增长速度为序，将以上各函数 $f(n)$ 排序，在其序号间加上“<”或“=”：

4 < 3 < 5 < 2 < 1

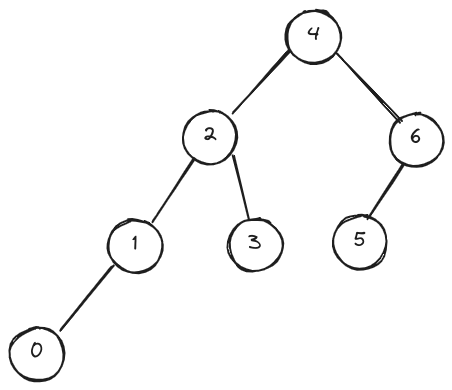
Fibonacci 树

所有内部节点均满足“左子树比右子树高一层”的二叉树，称作 Fibonacci 树。

1. 试画出其中高度为4者，并从0开始按中序遍历次序对各节点编号；

2. 试给出该树的层次遍历序列。

4 2 6 1 3 5 0

Related Search

我们知道，插值查找、二分查找、顺序查找分别适用于大、中、小规模的数据。当有序向量很长时，我们可以依次使用它们做接力式的查找。若在某系统中经测量确认，三种算法的时间复杂度常系数约为1280：64：1， 试估算出分别应在查找范围缩小到多大时切换算法（忽略复杂度的低次项、算法切换过程的时间消耗等因素）。

根据题意，插值查找的时间复杂度为 1280loglogn，二分查找时间复杂度为 64logn，顺序查找时间复杂度为 n。因此可以估计查找范围： 1280loglogn = 64logn → n=10

64logn = n → n=10

Failstone

Failstone (p, q){
	while (p != q)
		if (p > q) {
			int r = q;
			q = p;
			p ­= r;
		} else {
			(q&1) ? p <<=1 : q >>= 1;
		}
 }

1. 考察如上算法。对于 Failstone (5,13)，试列出每次执行到第 2 行（循环入口）时 p 和 q 的数值（退出后留空）：

    0   1   2   3   4   5   6   7   8   9   10  11  12   13
p   5  10  20   7   7   7   2   4   8   1   1   1   1
q  13  13  13  20  10   5   7   7   7   8   4   2   1(退出)

2. 试证明，该算法必然终止（不考虑整数溢出等因素）。

不会证。不过根据邓公的 PPT，通常步骤是： 单调性 + 不变性 + 找出观察量（通常是“周期”）

Queap 压缩

Queap 中原队列 Q 有对应的辅助队列 P，辅助队列用以存放 Q 的后缀的最大值，并且允许队尾插入和删除两种操作。对 P 进行压缩，得影子队列 P’

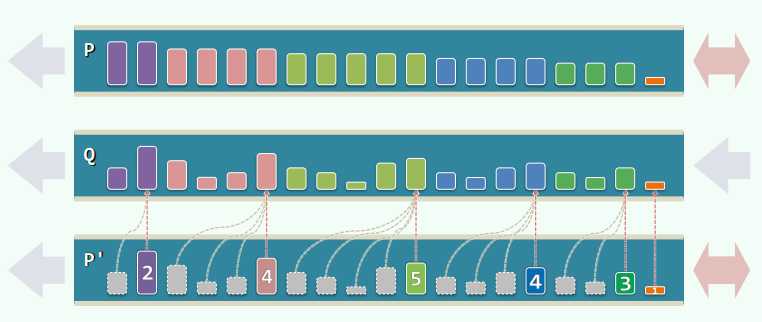
1. 举例证明 P’最坏的空间复杂度仍可能为 O (n)；（严格递减）

010101010… 串的影子队列的复杂度为 $\frac{n}{2}=O(n)$

2. 求 P'.size() 的期望

盲猜 logn，但是不会证。

Optimal Memorization

采用“记忆化”技术，可将递归式 fib(n)算法的时间复杂度从 $O({\varphi }^n)$ 降低至 $O(n)$ 。 现假定只能使用常数容量的记忆表 M[]，仅足以记忆 2m 个子问题的解，其余子问题依然需要进行递归。

1. 为使计算 fib(n)所需的递归次数（渐进意义上）总体最少，应选择记忆哪 2m 个子问题的解（ n >> m ）？

习题 1-19：fib(k)二分递归实例出现次数问题 该题证明，对 fib 的递归实例 fib(k)，其在计算过程中出现次数为 $F(k)=fib(n-k-1)$ 次，因此随着 k 的增加，出现次数逐渐降低。因此应当记忆越靠近底层的 fib 实例，越能减少所需递归次数。故应记忆 fib (2), fib (3),… fib (2m+1) 这 2m 个问题的解。

2. 证明你的结论